Exkurs Region, Distanz und räumlicher Einfluß
Geodaten sind prinzipiell wie gewöhnliche Daten zu betrachten. Allerdings sind die Aspekte der Skala, der Zonierung (aggregierte Flächeneinheiten), der Topologie (der Lage im Verhältnis zu anderen Entitäten) der Geometrie (Entfernung zueinander) eine Ableitung aus der Grundeigenschaft dass Geodaten eine Position im Raum besitzen.
Im Rahmen der räumlichen Statistik wirft das Fragen der räumlichen Autokorrelation bzw. Inhomogenität auf. Also letztlich Fragen welche Raumkonstruktion auf welcher Skala einen Einfluss auf meine Fragestellung hat.
Die klassischen Bereiche der räumlichen Statistik sind Punktmusteranalyse, Regression und Inferenz mit räumlichen Daten, dann die Geostatistik (Interpolation z.B. mit Kriging) sowie Methoden zur lokalen und globalen Regression und Klassifikation mit räumlichen Daten.
Nahezu alle dieser Bereiche basieren auf Daten die als Vektordatenmodell vorliegen. Das heisst es handelt sich um diskrete Geoobjekte die Null-, Ein- bzw. Zwei-dimensional Raumeigenschaften aufweisen.
Lernziele
Die Lernziele des Exkurs zur zweiten Übung sind:
- Verständnis für die konzeptionellen Hintergründe der Begriffe Region, Distanz und räumlicher Einfluss bezogen auf die jeweilig verfügbaren Datenmodelle
- Datenmanipulation und Nutzen von R
- Erstellen und Nutzung von räumlichen Datenmodellen (Raster- und Vektordaten) für die Alltagsarbeit
Einrichten der Umgebung
rm(list=ls())
rootDIR="~/Schreibtisch/spatialstat_SoSe2020/"
## laden der benötigten libraries
# wir definieren zuerst eine liste mit den Paketnamen und
# nutzen dann eine for schleife die jedes element aus der liste nimmt
# und schaut ob es bereits installiert ist utils::installed.packages()
# falls nicht wird es installiert
libs= c("sf","mapview","tmap","ggplot2","RColorBrewer","jsonlite","tidyverse","spdep","spatialreg","ineq", "tidygeocoder","usedist","raster","kableExtra")
for (lib in libs){
if(!lib %in% utils::installed.packages()){
utils::install.packages(lib)
}}
# nicht wundern lapply()ist eine integrierte for Schleife die alle im vector libs
# enthaltenen packages lädt indem sie den package Namen als character string an die
# function library übergibt
invisible(lapply(libs, library, character.only = TRUE))
Regionalisierung oder Aggregationsräume
Die Analyse der räumlichen Daten erfolgt oft in regionaler oder Aggregierung. Auch wenn alle am Liebsten Daten auf einer möglichst hoch aufgelösten Ebene verfügbar hätten (im besten Fall Einzelpersonen, Haushalte, Grundstücke, Briefkästen etc.) ist der Regelfall, dass es sich um räumlich (und zeitlich) aggregierte Daten handelt. Statt tägliche Daten über den Cornfllakes-Kosum in jeden Haushalt haben wir den Jahresmittelwert aller verkauften Zerealien in einem Bundesland. So geht das mit den meisten Daten, die zudem oft unterschiedlich aggregiert sind wo in Europa z.B. nationale und subnationale Einheiten (z.B. NUTS1, NUTS3, NUTS3, AMR etc.) vorliegen. Häufig gibt es auch räumliche Datensätze die in Form von Rasterzellenwerten quasi-kontinuierlich vorliegen.
Bei der visuellen Exploration aber auch bei der statistischen Analyse ist es von erheblichem Einfluss wie die Gebiete zur Aggregation der Daten geschnitten sind. Da dieser Zusammenhang eher willkürlich (auch oft historisch oder durch wissenschaftlich begründet) ist, sind die Muster, die wir sehen äußerst subjektiv. Dieses sogenannte Problem der veränderbaren Gebietseinheit (Modifiable Areal Unit Problem, MAUP) bezeichnet. Der Effekt von höheren Einheiten auf niedrigere zu schließen ist hingegen als ökologische Inferenz (Ecological Inference) bekannt.
Betrachten wir diese Zusammenhänge einmal ganz praktisch mit unserem Datensatz.
Um den Zusammenhang von Zonierung und Aggregation grundsätzlich zu verstehen erzeugen wir einen synthesischen Datensatz, der eine Region (angenommen wird die gesamte Ausdehnung Deutschlands) mit 10000 Haushalten enthält. Für jeden Haushalt ist der Ort und sein Jahreseinkommen bekannt. In einem nächsten Schritt werden die Daten in unterschiedliche Zonen aggregiert. Zunächst werden die nuts3_kreise eingeladen. Sie dienen der Georefrenzierung der Beispiel-Daten. Zunächst wir ein Datensatz von 10k zufällig über dem Gebiet Deutschlands verteilter Koordinaten erzeugt. Diesem werden dann zufällige Einkommensdaten zugewürfelt.
GI-konzeptionell erzeugen wir jetzt Tabellen die einerseits die Variable xy als Geokoordinate andererseits in der Variablen haushalts_einkommen eine Merkmalsausprägung in Form von Haushaltseinkommen enthalten. Da wir die Ausdehnung des nuts3_kreise Datensatz benutzen sind diese Daten auf Deutschland geokodiert. Streng genommen handelt es sich darum bereits um ein vollständigen Geodaten-Datensatz.
rootDIR="~/Schreibtisch/spatialstatSoSe2020/"
# einlesen der nuts3_kreise
nuts3_kreise = readRDS(file.path(rootDIR,"nuts3_kreise.rds"))
# für die Reproduzierbarkeit der Ergebnisse muss ein beliebiger `seed` gesetzt werden
set.seed(0)
nhh = 1000
# Normalverteilte Erzeugung von zufälligen Koordinatenpaaren
# in der Ausdehnung der nuts3_kreise Daten
# mit cbind() wird die einzelne Zahl des Breiten und des
# Längengrads in zwei verbundene Spalten geschrieben
# runif(10000,) erzeugt 10000 Zahlen innerhalb der Werte extent()
xy <- cbind(x=runif(nhh , extent(nuts3_kreise)[1], extent(nuts3_kreise)[3]), y=runif(nhh, extent(nuts3_kreise)[2], extent(nuts3_kreise)[4]))
# Normalverteilte Erzeugung von Einkommensdaten
haushalts_einkommen = runif(1000) * 10*runif(1000)
Nachdem die Daten erzeugt wurden, schauen wir und die akkumulierte, klassifizierte und räumliche Verteilung der Daten an.
# Festlegen der Grafik-Ausgabe
par(mfrow=c(1,3), las=1)
# Plot der sortieren Einkommen
plot(sort(haushalts_einkommen), col=rev(terrain.colors(nhh)), pch=20, cex=.75, ylab='Einkommen/Haushalt',xlab='Haushalte')
# Histogramm der Einkommensverteilung
hist(haushalts_einkommen, main='', col=rev(terrain.colors(10)), xlim=c(0,max(haushalts_einkommen)), breaks=seq(0,max(haushalts_einkommen)+1,1),xlab="Einkommen/Haushalt",ylab="Anzahl")
# Räumlicher Plot der Haushalte, Farbe und Größe markieren das Einkommen
plot(xy, xlim=c(extent(nuts3_kreise)[1], extent(nuts3_kreise)[3]), ylim=c(extent(nuts3_kreise)[2], extent(nuts3_kreise)[4]), cex=haushalts_einkommen/2, col=rev(terrain.colors(10)[round(haushalts_einkommen,0) + 1]), xlab="Rechtwert",ylab="Hochwert" )
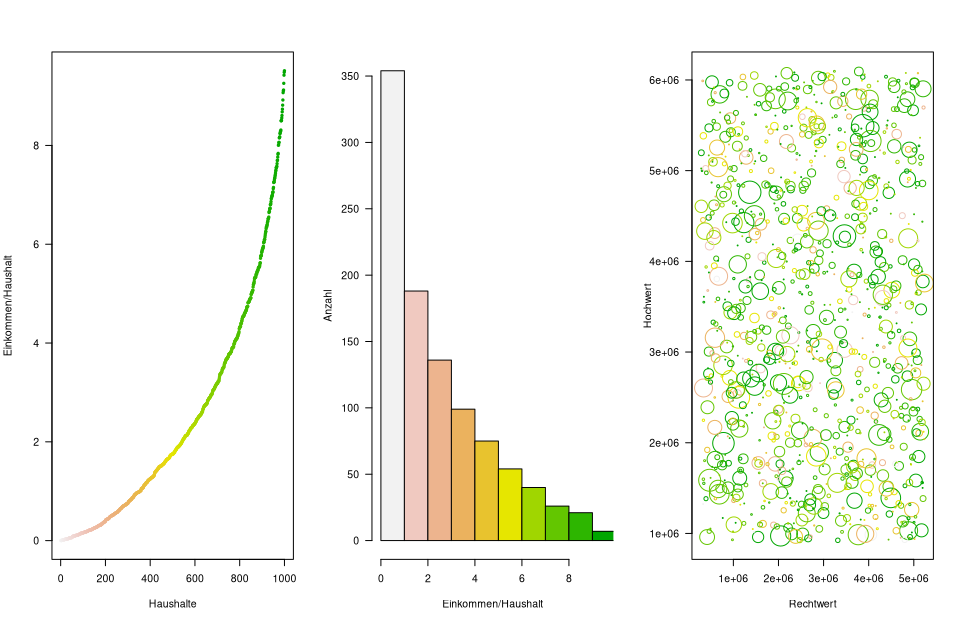
Abbildung 04-02-01: Die sortierte, aggregierte und räumliche Einkommensverteilung
Gini-Koeffizient und Lorenz-Kurve sind eine häufig gebrauchte erste Einschätzung um die Ungleichheit bzw. relative Konzentrationen von Verteilungen zu ermitteln.
# Berechnung Gini Koeffizient
ineq(haushalts_einkommen,type="Gini")
## [1] 0.4992696
# Plot der Lorenz Kurve
par(mfrow=c(1,1), las=1)
plot(Lc(haushalts_einkommen),col="darkred",lwd=2)
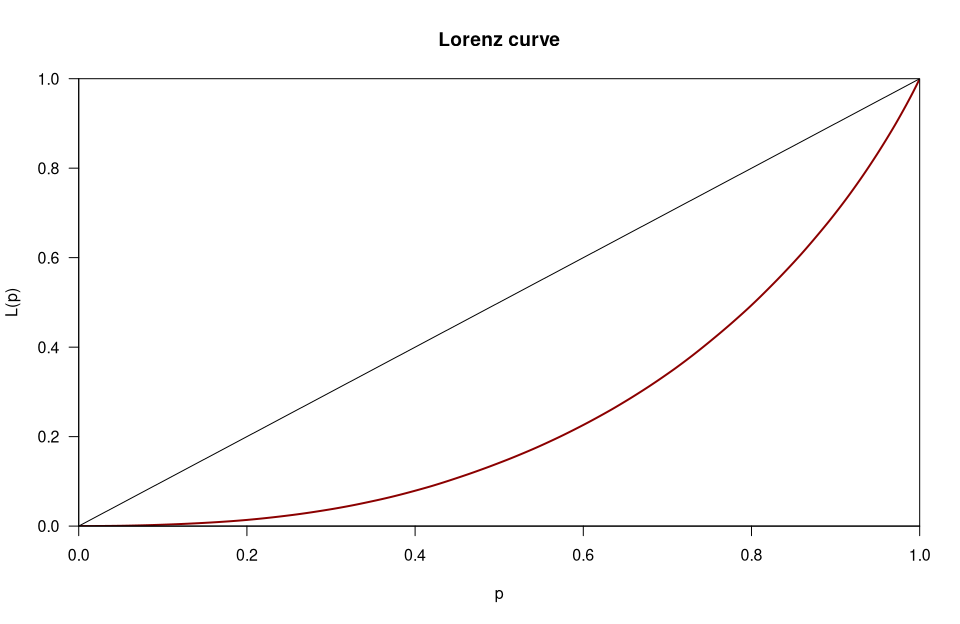
Abbildung 04-02-02: Lorenz-Kurve der Einkommensverteilung
Um die Bedeutung unterschiedlicher Regionen in Bezug auf die aggregierten Daten zu zeigen werden mit Hilfe des raster Pakets neun unterschiedliche Regionalisierungen mit der Ausdehnung und Georeferenzierung von Deutschland erzeugt.
GI-konzeptionell erzeugen wir jetzt ein kontinuierliches Raster das aus einer Anzahl von Reihen (nrow) und Spalten (ncol) besteht. Diesem leeren Raster wird die Ausdehnung und Georefrenzierung aus unserem bereits als sf Geoobjekt exisistierenden nuts3_kreise zugewiesen (xmn=extent(nuts3_kreise)[1]…). Schliesslich werden die zuvor erzeugten Werte (Variable haushalts_einkommen) an den Positionen xy) in diese leeren Raster einggetragen. Fertig ist ein Geodatensatz im Rasterdatenmodell.
# erzeugen von 9 künstlichen geometischen Regionen
# festlegen der Ausdehnung auf die Ausdehnung des nuts_3kreise Geoobjekts
xmn=extent(nuts3_kreise)[1]
xmx=extent(nuts3_kreise)[3]
ymn=extent(nuts3_kreise)[2]
ymx=extent(nuts3_kreise)[4]
# Definition der Region als Zeilen und Spalten Matrizen
regio_matrix = rbind(c(1,4),c(4,1),c(2,2),c(5,5),c(10,10),c(20,20),c(50,50),c(100,100),c(200,200))
# für 1 bis Anzahl der Elemente in regio_matrix wiederhole
rr=lapply(1:nrow(regio_matrix),function(x){
# erezuge Raster mit der Anzahl von Zeilen und Spalten
# sowie der Ausdehnung nuts3_kreise
r = raster(ncol=regio_matrix[x,][1], nrow=regio_matrix[x,][2], xmn=xmn, xmx=xmx, ymn=ymn, ymx=ymx)
# weise dem Raster seine Georefrenzierung zu
crs(r) = sp::CRS("+init=epsg:25832")
# lese die Einkommenswerte in Raster wenn notwendig mittle die Werte
r = rasterize(xy, r, haushalts_einkommen, mean)
})
Die einzelnen Grafiken verdeutlichen wie die räumliche Anordnung der Zonen verteilt ist. Es handelt sich um 2 Streifenzonierungen und 7 unterschiedlich aufgelöste Gitter von 4x4, 5x5, 10x10, 20x20, 50x50 und 100x100 Regionen.
# Festlegen der Grafik-Ausgabe
par(mfrow=c(3,3), las=1)
# Plotten der 9 Regionen
# in main wird der Titel für jede Grafik definiert
for (i in 1:length(rr)){
plot(rr[[i]],main=paste0("ncol=",regio_matrix[i][1]," nrow=",regio_matrix[i][1]))
}
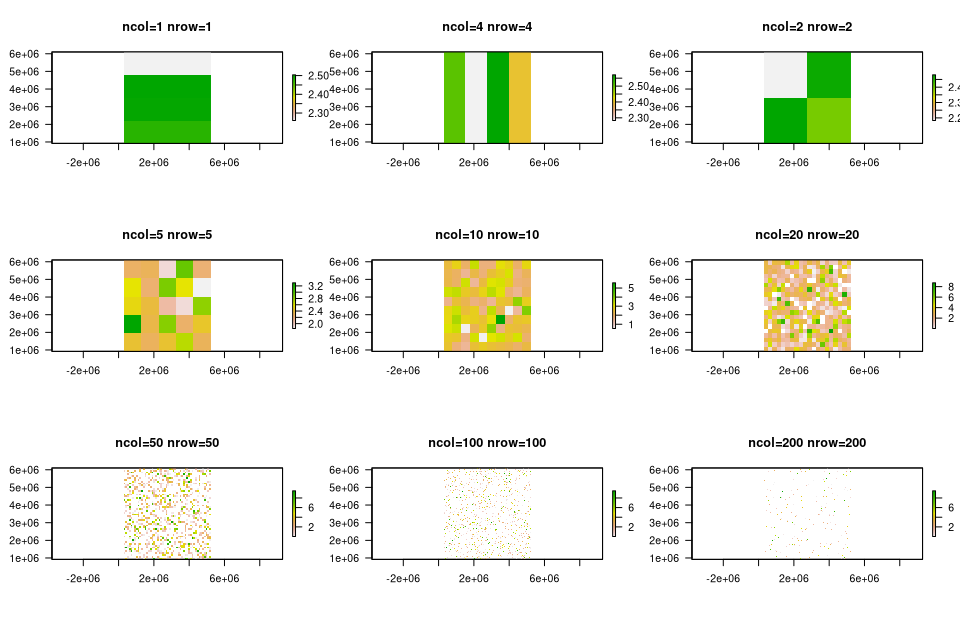
Abbildung 04-02-03: 3x3 Matrix der unterschiedlichen Zonen-Anordnungen
Wenn man nun die korrespondierenden zonalen Histogramme anschaut, wird deutlich wie sehr eine Zonierung die Verteilung der Ergebnisse im Raum beeinflusst.
# Festlegen der Grafik-Ausgabe
par(mfrow=c(3,3), las=1)
# Plotten der zugehörigen Histogramme
for (i in 1:length(rr)){
hist(rr[[i]],main=paste0("ncol=",regio_matrix[i][1]," nrow=",regio_matrix[i][1]),
col=rev(terrain.colors(10)), xlim=c(0,max(haushalts_einkommen)), breaks=seq(0,max(haushalts_einkommen)+1,1),xlab="Einkommen/Haushalt",ylab="Anzahl")
}
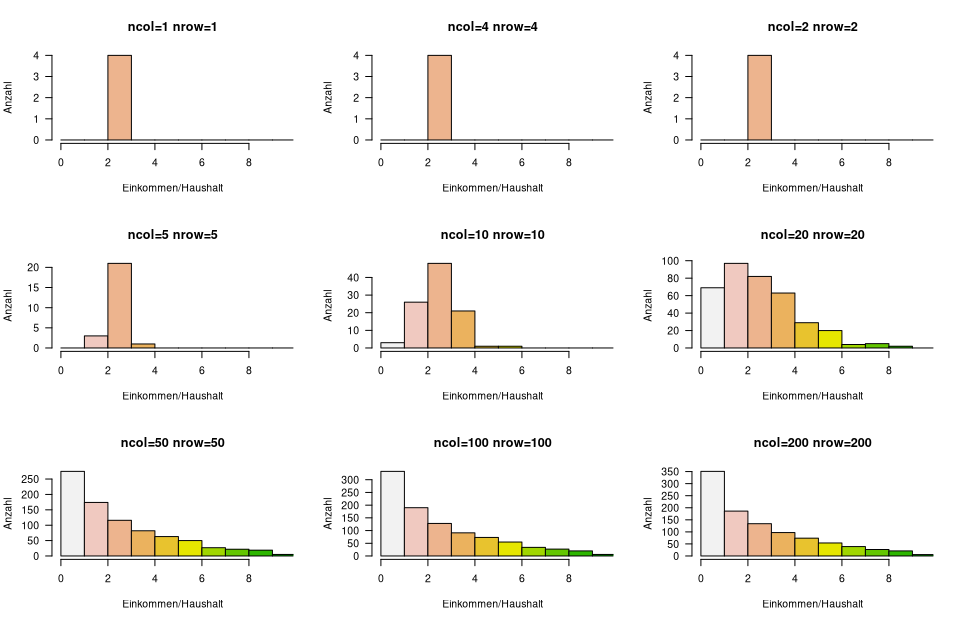
Abbildung 04-02-04: 3x3 Matrix der unterschiedlichen Zonen-Histogramme
Distanz
Als Distanz wird die Entfernung von zwei Positionen bezeichnet. Sie kann zunächst einmal als ein zentrales Konzept der Geographie angenommen werden. Erinnern sie sich an Waldo Toblers ersten Satz zur Geographie, dass “alles mit allem anderen verwandt ist, aber nahe Dinge mehr verwandt sind als ferne Dinge”. Die Entfernung ist scheinbar sehr einfach zu bestimmen. Natürlich können wir die Entfernung auf eine isometrischen und isomorhpen Fläche mittels der “Luftlinie” (euklidische Distanz) berechnen. Zentrales Problem ist das diese Betrachtung häufig wenn in der Regel nicht relevant ist. Es gibt nicht nur (nationale) Grenzen, Gebirge oder beliebige andere Hindernisse, die Entfernung zwischen A und B kann auch asymmetrisch sein (bergab geht’s einfacher und schneller als bergauf). Das heißt Distanzen können auch über z.B. Distanzkosten gewichtet werden.
Üblicherweise werden Distanzen in einer “Distanzmatrix” dargestellt. Eine solche Matrix enthält als Spaltenüberschriften und als Zeilenbeschriftung die Kennung von jedem berechneten Ort. Im jedem Feld wird die Entfernung eingetragen. Für kartesische Koordinaten erfolgt dies einfach über den Satz des Pythagoras.
Betrachten wir diese Zusammenhänge einmal ganz praktisch:
Berechnen der Distanz-Matrix
Wir erstellen für eine Anzahl Punkte eine Distanzmatrix. Wenn die Positionen in Länge/Breite angegeben sind wird es deutlich aufwendiger. In diesem Fall können wir die Funktion pointDistance aus dem raster Paket verwenden (allerdings nur wenn das Koordinatensystem korrekt angegeben wird). Eleganter ist jedoch die Erzeugung von Punktdaten als sf Objekt. Es ist leicht möglich beliebige reale Punktdaten mit Hilfe des tidygeocoder Pakets zu erzeugen. Wir geben lediglich eine Städte oder Adressliste an.
GI-konzeptionell erzeugen wir jetzt ein Vektordatenmodell das aus einer Anzahl von Koordinaten besteht. Anderes als in der Eingangsübung nutzen wir diesmal Städtenamen (Merkmalsausprägung) und einen Webservice der die passenden Koordinaten abfragt (Positionen). In der lapply Schleife werden diese abgefragt und als sf Objekt zusammengefügt. Fertig ist ein Geodatensatz im Vektordatenmodell.
Erzeugen einer geokodierten Punktliste
Zur direkten Überprüfung ob die Punkte richtig geokodiert sind eignet sich nach Erzeugung des Punkte-Objekts die Funktion mapview hervorragend.
# Erzeugen von beliebigen Raumkoordinaten
# mit Hilfe von tidygeocoder::geo_osm und sf
# Städteliste
staedte=c("München","Berlin","Hamburg","Köln","Bonn","Hannover","Nürnberg","Stuttgart","Freiburg","Marburg")
# Abfragen der Geokoordinaten der Städte mit eine lapply Schleife
# 1) die Stadliste wird in die apply Schleife (eine optimierte for-Schleife) eingelesen
# 2) für jeden Namen (X) in der Liste wird mit geo_osm die
# Koordinate ermittelt Die in eckigen Klammern angegebne Position 2
# ist die Latitude (geo_osm(x)[2]) [1] enstprechend die Longitude
# 3) Umwandlung in numerische Werte
# 4) Jedes latlon Paar wird in einen sf-Punkt konvertiert und
# gleichzeitig das korrekte Georefrenzierungssystem zugewiesen (cres = 4326)
# 5) Zuletzt werden an die Koordinatenpaare die Städtenamen angehangen
coord_city = lapply(staedte, function(x){
latlon = c(geo_osm(x)[2],geo_osm(x)[1])
class(latlon) = "numeric"
p = st_sfc(st_point(latlon), crs = 4326)
st_sf(name = x,p)
})
# Umwandeln der aus der lapply Schleife zurückgegebnen Liste in eine Matrix
geo_coord_city = do.call("rbind", coord_city)
saveRDS(geo_coord_city,"geo_coord_city.rds")
# visualize with mapview
mapview(geo_coord_city, color='red',legend = FALSE)
Abbildung 04-02-05: Webkarte mit den erzeugten Punktdaten. In diesem Falle zehn nicht ganz zufällige Städte Deutschlands
R-Training
Erzeugen Sie aus dem xy Datensatz des ersten Beipiels ein sf Objekt.
Plotten der Daten mit der plot Funktion
Die klassische Variante mit der plot Funktion ist ist zwar für den Alltag sehr einfach zu nutzen aber für das Erstellen anspruchsvollerer Grafiken oder Karten aber im Detail doch sehr aufwändig. Da wir es hier mit einem R Vektorobjekt des Paket sf zu tun haben kann die “Veteran-Funktion” plot() nicht direkt mit den Koordinaten umgehen. Hierfür nutzen wir die Funktion st_coordinates() die auf die Koordinatenpaare zugreift und diese als Matrix zurückgibt. Da es sich um einen data.frame (also die R-Tabelle) handelt kann mit den eckigen Klammern beliebig auf Spalten zugegriffen werden.
# klassisches Plotten eines sf Objects erfordert den Zugriff auf die Koordinatenpaare
# mit Hilfe der Funktion st_coordinates(geo_coord_city) leicht möglich
# schliesslich wird mit der Funktion text() die Beschriftung hinzugefügt
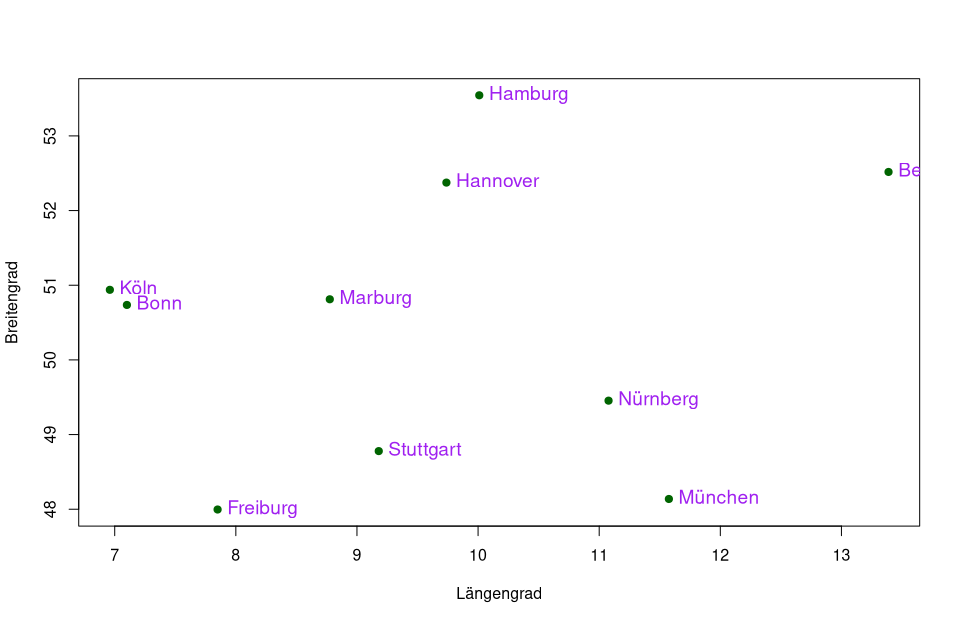
plot(st_coordinates(geo_coord_city),
pch=20, cex=1.5, col='darkgreen', xlab='Längengrad', ylab='Breitengrad')
text(st_coordinates(geo_coord_city), labels = staedte, cex=1.2, pos=4, col="purple")
R-Training
Mit Hilfe der Funktion min(st_coordinates(geo_coord_city)[,1]) kann der Minimum-X-Wert ermittelt werden. Analog gilt das für die übrigen Werte. Das Aufaddieren von 0.5 dient nur der besseren Platzierung der Beschriftung. Bauen sie die unten auskommentierten so in den Plot-Befehl ein, dass die Beschriftung von Berlin sichtbar wird. Besdenken Sie dass die einzelnen Elemente des Plot Befehls wie in einer Liste durch Kommata getrennt werden.
## mit Hilfe der Funktion min(st_coordinates(geo_coord_city)[,1]) werden
## minimum und maximum Ausdehnung bestimmt
## xlim und ylim sind die Minimum und Maximum Koordinaten der Plotausdehnung
# xlim = c(min(st_coordinates(geo_coord_city)[,1]) - 0.5
# ,max(st_coordinates(geo_coord_city)[,1]) + 0.5)
# ylim = c(min(st_coordinates(geo_coord_city)[,2]) - 0.5
# ,max(st_coordinates(geo_coord_city)[,2]) + 0.5)
Abbildung 04-02-06: Klassische Plot-Ausgabe mit den erzeugten Punktdaten. Erneut zehn nicht ganz zufällige Städte Deutschlands
Distanzberechnung von Geokoordinaten
Die Berechnung der Distanzen zwischen den 10 Städten greift einigermaßen tief in Geodaten-Verarbeitung ein. Die Punkte werden über die Funktion tidygeocoder::geo_osm mit Hilfe der Stadtnamen erzeugt. Standardisiert werden Kugelkoordinaten (also geographische Koordinaten) erzeugt also Längen und Breitengrade auf Grundlage des WGS84 Datum. Auf einem Ellipsoid ist es deutlich aufwendiger (oder fehlerträchtiger) Entfernungen zu rechnen als in in einem projizierten (also kartesischen) Koordinatensystem da hier sphärische Trigonometrie im Gegensatz zum Satz des Pythagoras zur Anwendung kommt.
Daher transformieren wir zunächst den Datensatz in das amtlich gültige Referenzsystem für Deutschland nämlich ETRS89/UTM. Zur Zuweisung werden viele konkurrierende Systeme verwendet. Im nachstehenden Beispiel nutzen wir die EPSG Konvention. Für das zuvor genannte System ist das der EPSG-Code 25832.
# Zuerst projizieren wir den Datensatz auf ETRS89/UTM
proj_coord_city = st_transform(geo_coord_city, crs = 25832)
# nun berechnen wir die Distanzen
city_distanz = dist(st_coordinates(proj_coord_city))
# mit Hilfe von dist_setNames können wir die Namen der distanzmatrix zuweisen
dist_setNames(city_distanz, staedte)
## München Berlin Hamburg Köln Bonn Hannover Nürnberg
## Berlin 504156.6
## Hamburg 611337.7 253841.6
## Köln 456511.6 477393.1 356810.5
## Bonn 434329.5 478145.8 370325.9 24607.7
## Hannover 489061.8 248686.4 131348.9 249893.3 258162.1
## Nürnberg 150928.4 377495.0 460900.6 337014.5 318118.3 338167.6
## Stuttgart 190926.8 511243.2 533104.9 288316.8 264173.9 401815.7 157508.4
## Freiburg 278029.8 639022.5 635366.9 333440.4 309440.8 505124.9 287407.8
## Marburg 359924.1 371191.0 315365.1 128538.4 118421.0 186154.7 223271.1
## Stuttgart Freiburg
## Berlin
## Hamburg
## Köln
## Bonn
## Hannover
## Nürnberg
## Stuttgart
## Freiburg 131404.0
## Marburg 227925.4 320161.6
round(city_distanz,0)
## 1 2 3 4 5 6 7 8 9
## 2 504157
## 3 611338 253842
## 4 456512 477393 356811
## 5 434330 478146 370326 24608
## 6 489062 248686 131349 249893 258162
## 7 150928 377495 460901 337014 318118 338168
## 8 190927 511243 533105 288317 264174 401816 157508
## 9 278030 639023 635367 333440 309441 505125 287408 131404
## 10 359924 371191 315365 128538 118421 186155 223271 227925 320162
Wir erzeugen aus der Distanz-Matrix class = dist eine normale R-Matrix. Leider müssen dann die Namen wieder zugewiesen werden.
# make a full matrix an
city_distanz <- as.matrix(city_distanz)
rownames(city_distanz)=staedte
colnames(city_distanz)=staedte
# Ausgabe einer hübscheren Tabelle mit kintr::kable
# die Notation mit ist das sogennante "pipen" aus der tidyverse Welt
# hier werden die Daten und Verarbeitungsschritte von der erstenVariable in
# die nächste weitergeleitet
knitr::kable(city_distanz) %>%
kable_styling(bootstrap_options = "striped", full_width = F)
| München | Berlin | Hamburg | Köln | Bonn | Hannover | Nürnberg | Stuttgart | Freiburg | Marburg | |
|---|---|---|---|---|---|---|---|---|---|---|
| München | 0.0 | 504156.6 | 611337.7 | 456511.6 | 434329.5 | 489061.8 | 150928.4 | 190926.8 | 278029.8 | 359924.1 |
| Berlin | 504156.6 | 0.0 | 253841.6 | 477393.1 | 478145.8 | 248686.4 | 377495.0 | 511243.2 | 639022.5 | 371191.0 |
| Hamburg | 611337.7 | 253841.6 | 0.0 | 356810.5 | 370325.9 | 131348.9 | 460900.6 | 533104.9 | 635366.9 | 315365.1 |
| Köln | 456511.6 | 477393.1 | 356810.5 | 0.0 | 24607.7 | 249893.3 | 337014.5 | 288316.8 | 333440.4 | 128538.4 |
| Bonn | 434329.5 | 478145.8 | 370325.9 | 24607.7 | 0.0 | 258162.1 | 318118.3 | 264173.9 | 309440.8 | 118421.0 |
| Hannover | 489061.8 | 248686.4 | 131348.9 | 249893.3 | 258162.1 | 0.0 | 338167.6 | 401815.7 | 505124.9 | 186154.7 |
| Nürnberg | 150928.4 | 377495.0 | 460900.6 | 337014.5 | 318118.3 | 338167.6 | 0.0 | 157508.4 | 287407.8 | 223271.1 |
| Stuttgart | 190926.8 | 511243.2 | 533104.9 | 288316.8 | 264173.9 | 401815.7 | 157508.4 | 0.0 | 131404.0 | 227925.4 |
| Freiburg | 278029.8 | 639022.5 | 635366.9 | 333440.4 | 309440.8 | 505124.9 | 287407.8 | 131404.0 | 0.0 | 320161.6 |
| Marburg | 359924.1 | 371191.0 | 315365.1 | 128538.4 | 118421.0 | 186154.7 | 223271.1 | 227925.4 | 320161.6 | 0.0 |
Räumlicher Einfluss
Die beiden Aspekte zuvor haben die räumlichen Verhältnisse in Form von Raumabgrenzung und Distanz beschrieben. In der räumlichen Analyse ist es jedoch von zentraler Bedeutung den räumlichen Einfluss zwischen geographischen Objekten zu schätzen bzw. zu messen. Dies kann prozessorientiert funktional erfolgen, der oberliegende Teil eines Baches fließt in den unterliegenden. In der datengetriebenen Betrachtungsweise ist dies in der Regel eine Funktion der Nachbarschaft oder der (inversen) Entfernung. Um damit in statistischen Modellen arbeiten zu können werden diese Konzepte als räumliche Gewichtungsmatrix ausgedrückt.
Das generelle und schwerwiegende Problem ist, dass der räumliche Einfluss sehr komplex ist und faktisch nie gemessen werden kann. Daher gibt es zahllose Arten ihn zu schätzen.
Zum Beispiel kann der räumliche Einfluss von Polygonen aufeinander (z.B, NUTS3 Verwaltungsbezirke) so ausgedrückt werden, dass sie eine/keine gemeinsame Grenze, sie kann als euklidische Distanz zwischen ihren Schwerpunkten bestimmt werden oder über die Länge gemeinsamer Grenzen gewichtet werden und so fort.
Nachbarschaft
Die Nachbarschaft ist das vielleicht wichtigste Konzept. höherdimensionale Geoobjekte können als benachbart betrachtet werden wenn sie sich berühren, z.B. benachbarte Länder. Bei null-dimensionalen Objekten (Punkte) ist der gebräuchlichste Ansatz die Entfernung in Kombination mit einer Anzahl von Punkten für die Ermittlung der Nachbarschaft zu nutzen.
Betrachten wir diese Zusammenhänge einmal ganz praktisch:
Wir erstellen eine Nachbarschaftsmatrix für die oben erzeugten Punktdaten. Punkte seien benachbart, wenn sie innerhalb eines Abstands von z.B. 25 Kilometer liegen.
# Distanzmatrix für Entfernungen > 250 km
cd = city_distanz < 250000
# Ausgabe einer hübscheren Tabelle mit kintr::kable die Notation ist das sogenannte pipen aus der tidyverse Welt
knitr::kable(cd) %>%
kable_styling(bootstrap_options = "striped", full_width = F)
| München | Berlin | Hamburg | Köln | Bonn | Hannover | Nürnberg | Stuttgart | Freiburg | Marburg | |
|---|---|---|---|---|---|---|---|---|---|---|
| München | TRUE | FALSE | FALSE | FALSE | FALSE | FALSE | TRUE | TRUE | FALSE | FALSE |
| Berlin | FALSE | TRUE | FALSE | FALSE | FALSE | TRUE | FALSE | FALSE | FALSE | FALSE |
| Hamburg | FALSE | FALSE | TRUE | FALSE | FALSE | TRUE | FALSE | FALSE | FALSE | FALSE |
| Köln | FALSE | FALSE | FALSE | TRUE | TRUE | TRUE | FALSE | FALSE | FALSE | TRUE |
| Bonn | FALSE | FALSE | FALSE | TRUE | TRUE | FALSE | FALSE | FALSE | FALSE | TRUE |
| Hannover | FALSE | TRUE | TRUE | TRUE | FALSE | TRUE | FALSE | FALSE | FALSE | TRUE |
| Nürnberg | TRUE | FALSE | FALSE | FALSE | FALSE | FALSE | TRUE | TRUE | FALSE | TRUE |
| Stuttgart | TRUE | FALSE | FALSE | FALSE | FALSE | FALSE | TRUE | TRUE | TRUE | TRUE |
| Freiburg | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | TRUE | TRUE | FALSE |
| Marburg | FALSE | FALSE | FALSE | TRUE | TRUE | TRUE | TRUE | TRUE | FALSE | TRUE |
Gewichtungs-Matrix für Punkte
Anstatt den räumlichen Einfluss als binären Wert (also topologisch benachbart ja/nein) auszudrücken, kann er als kontinuierlicher Wert ausgedrückt werden. Der einfachste Ansatz ist die Verwendung des inversen Abstands (je weiter entfernt, desto niedriger der Wert).
# inverse Distanz
gewichtungs_matrix = (1 / city_distanz)
# inverse Distanz zum Quadrat
gewichtungs_matrix_q = (1 / city_distanz ** 2)
# Ausgabe einer hübscheren Tabelle mit kintr::kable die Notation ist das sogenannte pipen aus der tidyverse Welt
knitr::kable(gewichtungs_matrix) %>%
kable_styling(bootstrap_options = "striped", full_width = F)
| München | Berlin | Hamburg | Köln | Bonn | Hannover | Nürnberg | Stuttgart | Freiburg | Marburg | |
|---|---|---|---|---|---|---|---|---|---|---|
| München | Inf | 2.0e-06 | 1.6e-06 | 2.20e-06 | 2.30e-06 | 2.0e-06 | 6.6e-06 | 5.2e-06 | 3.6e-06 | 2.8e-06 |
| Berlin | 2.0e-06 | Inf | 3.9e-06 | 2.10e-06 | 2.10e-06 | 4.0e-06 | 2.6e-06 | 2.0e-06 | 1.6e-06 | 2.7e-06 |
| Hamburg | 1.6e-06 | 3.9e-06 | Inf | 2.80e-06 | 2.70e-06 | 7.6e-06 | 2.2e-06 | 1.9e-06 | 1.6e-06 | 3.2e-06 |
| Köln | 2.2e-06 | 2.1e-06 | 2.8e-06 | Inf | 4.06e-05 | 4.0e-06 | 3.0e-06 | 3.5e-06 | 3.0e-06 | 7.8e-06 |
| Bonn | 2.3e-06 | 2.1e-06 | 2.7e-06 | 4.06e-05 | Inf | 3.9e-06 | 3.1e-06 | 3.8e-06 | 3.2e-06 | 8.4e-06 |
| Hannover | 2.0e-06 | 4.0e-06 | 7.6e-06 | 4.00e-06 | 3.90e-06 | Inf | 3.0e-06 | 2.5e-06 | 2.0e-06 | 5.4e-06 |
| Nürnberg | 6.6e-06 | 2.6e-06 | 2.2e-06 | 3.00e-06 | 3.10e-06 | 3.0e-06 | Inf | 6.3e-06 | 3.5e-06 | 4.5e-06 |
| Stuttgart | 5.2e-06 | 2.0e-06 | 1.9e-06 | 3.50e-06 | 3.80e-06 | 2.5e-06 | 6.3e-06 | Inf | 7.6e-06 | 4.4e-06 |
| Freiburg | 3.6e-06 | 1.6e-06 | 1.6e-06 | 3.00e-06 | 3.20e-06 | 2.0e-06 | 3.5e-06 | 7.6e-06 | Inf | 3.1e-06 |
| Marburg | 2.8e-06 | 2.7e-06 | 3.2e-06 | 7.80e-06 | 8.40e-06 | 5.4e-06 | 4.5e-06 | 4.4e-06 | 3.1e-06 | Inf |
Wie auch die räumliche Gewichtung wird die Matrix oft zeilennormiert, das heißt dass die Summe der Gewichte für jede Zeile (Position oder Wert der Position) in der Matrix gleich ist.
# löschen der Inf Werte die durch den Selbstbezug der Punkte entestehen
gewichtungs_matrix <- as.matrix(gewichtungs_matrix)
rownames(gewichtungs_matrix)=staedte
colnames(gewichtungs_matrix)=staedte
gewichtungs_matrix[!is.finite(gewichtungs_matrix)] <- NA
zeilen_summe <- rowSums(gewichtungs_matrix, na.rm=TRUE)
zeilen_summe
## München Berlin Hamburg Köln Bonn Hannover
## 2.839529e-05 2.299421e-05 2.748176e-05 6.894169e-05 7.021031e-05 3.435182e-05
## Nürnberg Stuttgart Freiburg Marburg
## 3.481930e-05 3.715831e-05 2.915882e-05 4.222911e-05
Gewichtungs-Matrix für Polygone
Binäre 4-er Nachbarschaft
Die Gewichtungsmatrix für Polygone zu bestimmen ist natürlich etwas komplexer dafür gibt es allerdings mit spdep ein bewährtes Paket.
Die Funktion poly2nb kann unter anderem um eine Rook Nachbarschaftsliste erzeugen. Sie dient als Grundlage einer Nachbarschaftsmatrix.
rook = poly2nb(nuts3_kreise, row.names=nuts3_kreise$NUTS_NAME, queen=FALSE)
rook_ngb_matrix = nb2mat(rook, style='B', zero.policy = TRUE)
# Berechne die Anzahl der Nachbarn für jedes Gebiet
anzahl_nachbarn <- rowSums(rook_ngb_matrix)
# als prozentsatz
prozentzahl_nachbarn = round(100 * table(anzahl_nachbarn) / length(anzahl_nachbarn), 1)
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
main=paste("Binary neighbours", sep=""))
coords <- coordinates(as(nuts3_kreise,"Spatial"))
plot(rook, coords, col='red', lwd=2, add=TRUE)
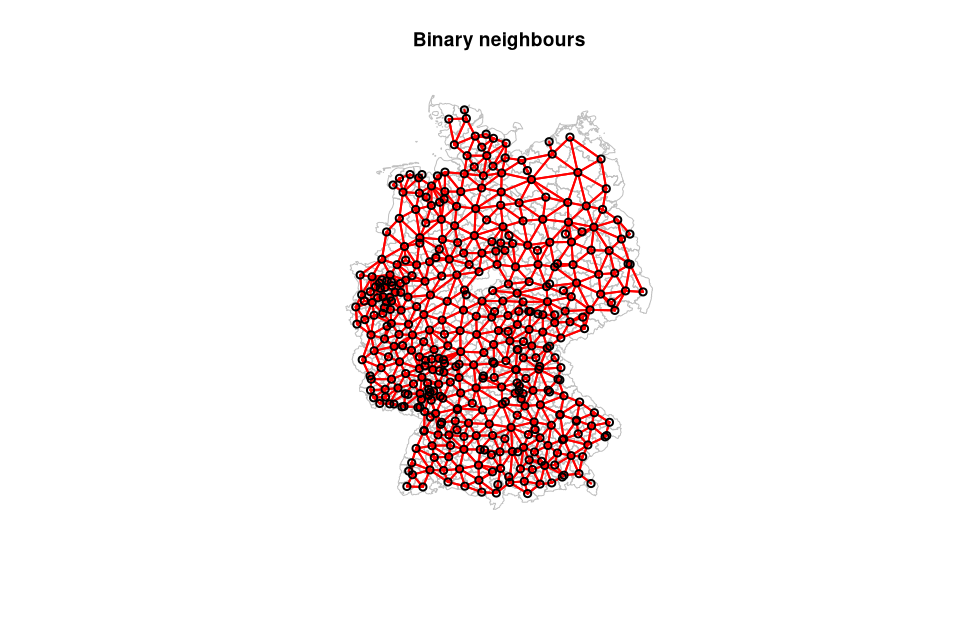
Abbildung 04-02-05: Binäre 4-er Nachbarschaft für die Landkreise Deutschlands
Nearest-Distance Nachbarn
Nachfolgend werden exemplarisch die 3 bzw. 5 nächsten Nachbarn zu einem Kreis ausgewiesen.
rn <- row.names(nuts3_kreise)
# Berechne die 3 und 5 Nachbarschaften
kreise_dist_k3 <- knn2nb(knearneigh(coords, k=3, RANN=FALSE))
kreise_dist_k5 <- knn2nb(knearneigh(coords, k=5, RANN=FALSE))
##
par(mfrow=c(1,2),las=1)
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
main=paste("Drei Nachbarkreise", sep=""))
plot(kreise_dist_k3, lwd = 1, coords, add=TRUE,col="blue")
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
main=paste("Fünf Nachbarkreise", sep=""))
plot(kreise_dist_k5, lwd =1, coords, add=TRUE,col="red")
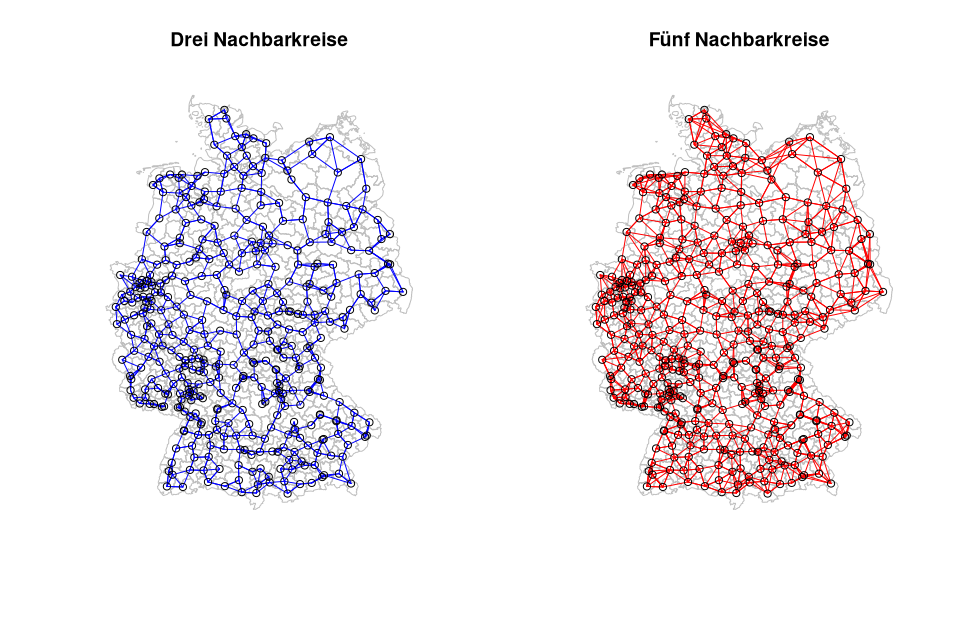
Abbildung 04-02-06:Nächste 3-er/5-er Nachbarschaft für die Landkreise Deutschlands
Distanz-basierte Nachbarschaft
Nachfolgend wird für den Mittelwert, das dritte Quartil und den Maximalwert der Distanzverteilung aller Kreis-Zentroide die Nachbarschaft bestimmt.
# berechne alle Distanzen für die Flächenschwerpunkte der Kreise
knn2nb = knn2nb(knearneigh(coords))
# erzeuge die Kreisdistanzen
kreise_dist <- unlist(nbdists(knn2nb, coords))
summary(kreise_dist)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1026 11485 20205 19811 26498 56096
rn <- row.names(nuts3_kreise)
# berechne die Nachbarschaften für alle Kreise < mean 3. Quartil und Max Wert
nachbarschaft_mean <- dnearneigh(coords, 0, summary(kreise_dist)[4], row.names=rn)
nachbarschaft_max <- dnearneigh(coords, 0, summary(kreise_dist)[6], row.names=rn)
nachbarschaft_thirdQ <- dnearneigh(coords, 0, summary(kreise_dist)[5], row.names=rn)
# Plotten der drei Distanzen
par(mfrow=c(1,3), las=1)
# Maxwert
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
main=paste("Nachbarkreise näher ",round(summary(kreise_dist)[6],0) ," km", sep=""))
plot(nachbarschaft_max, lwd =1,coords, add=TRUE,col="green")
# 3. Quartil
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
main=paste("Nachbarkreise näher ",round(summary(kreise_dist)[5],0) ," km", sep=""))
plot(nachbarschaft_thirdQ, lwd = 2, coords, add=TRUE,col="red")
# Mittelwert
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
main=paste("Nachbarkreise näher ",round(summary(kreise_dist)[4],0) ," km", sep=""))
plot(nachbarschaft_mean, lwd =3, coords, add=TRUE,col="blue")

Abbildung 04-02-07: Distanzbasierte Nachbarschaften für die Landkreise Deutschlands, a) Nachbarschaften innerhalb der Maximaldistanz der Distanzmatrix, b) Nachbarschaften innerhalb der 3. Quartils der Distanzmatrix, c) b) Nachbarschaften innerhalb der Mittelwerts der Distanzmatrix
Was ist sonst noch zu tun?
Versuchen Sie sich zu verdeutlichen, dass die Mehrzahl der räumlichen Regressions-Analysen und -Modelle auf den Grundannahmen dieser Übung basieren. Das heisst es kommt maßgeblich auf Ihre konzeptionellen oder theoriegeleiteten Vorstellungen an, welche Nachbarschaft, welches Nähe-Maß und somit auch, welche räumlichen Korrelationen zustande kommen. Bitte beschäftigen Sie sich mitdem Skript.
- versuchen sie sich an den R-Trainings. Sie sollen Sie zum aktiven Umgang mit
Rermuntern. - gehen Sie die Skripte schrittweise durch. Lassen Sie es nicht von vorne bis hinten unkontrolliert durchlaufen
- gleichen Sie ihre Kenntnisse aus dem Statistikkurs mit diesen praktischen Übungen ab und identifizieren Sie was Raum-Wirskamkeiten sind.
- spielen Sie mit den Einstellungen, lesen Sie Hilfen und lernen Sie schrittweise die Handhabung von R kennen.
- lernen Sie quasi im “Vorbeigehen” wie Daten zu plotten sind oder wann Sie ein wenig Acht geben müssen wenn Sie mit Geodaten arbeiten (viele Hinweise und Erläuterungen sind in den Kommentarzeilen untergebracht).
-
Versuchen Sie sich mit der Datenvisualisierung vertraut zu machen. Hierzu können Sie die Vignetten von
tmapundmapviewnutzen. tmap, mapview - stellen Sie Fragen im Forum, im Kurs oder per email mit dem Betreff [M&S2020]
Wo gibt’s mehr Informationen?
Für mehr Informationen kann unter den folgenden Ressourcen nachgeschaut werden:
-
Spatial Data Analysis von Robert Hijmans. Sehr umfangreich und empfehlenswert. Viel der Beispiele basieren auf seiner Vorlesung und sind für unsere Verhältnisse angepasst.
-
Der UseR! 2019 Spatial Workshop von Roger Bivand. Roger ist die absolute Referenz hinischtlich räumlicher Ökonometrie mit R. Er hat unzählige Pakete geschrieben und ebensoviel Schulungs-Material und ist unermüdlich in der Unterstützung der Community.
Download Skript
Das Skript kann unter unit04-01_sitzung.R heruntergeladen werden