Sitzung 4 - Räumliche Regression Workflow

Die übliche Vorgehensweise bei der Regressionsanalyse wurde in den vergangenen drei Sitzungen dargestellt. Sie folgt in der Regel einer festen Reihenfolge: der Datenaquise und -vorverarbeitung folgt die Betestung der Daten auf Verteilung Normalität etc. und schliesslich die Ableitung von geeigneten Regressionsmodellen zur Vorhersage von Variablen. Kommt der räumlich eAspekt hinzu beginnt hier eine relativ aufwendige Prozedur um festzustellen welcher Anteil der Vorhersage räumliem einfluss geschuldet ist. Liegt eine räumliche Autokorrelation der Daten vor sind p-Werte und Regressionsmodell-Koeffizienten nicht verlässlich. Daher erfolgt die Untersuchung bzw. Modellierung mit räumlichem Einfluss mit Hilfe von geeigneten Modellen. Hier werden in aller Kürze das Spatial autoregressive model (SAR) Moell bzw. das Spatial Error Model (SEM) vorgestellt.

Einrichten der Umgebung

rm(list=ls())
rootDIR="~/Schreibtisch/spatialstat_SoSe2020/"
## laden der benötigten libraries
# wir definieren zuerst eine liste mit den Paketnamen und 
# nutzen dann eine for  schleife die jedes element aus der  liste nimmt 
# und schaut ob es bereits installiert ist utils::installed.packages() 
# falls nicht wird es installiert 
libs= c("sf","mapview","tmap","spdep","ineq","cartography","spatialreg", "tidygeocoder","usedist","raster","kableExtra","downloader","rnaturalearthdata")
for (lib in libs){
  if(!lib %in% utils::installed.packages()){
    utils::install.packages(lib)
  }}
# nicht wundern lapply()ist eine integrierte for Schleife die alle im vector libs
# enthaltenen packages lädt indem sie den package Namen als character string an die 
# function library übergibt
invisible(lapply(libs, library, character.only = TRUE))

#---------------------------------------------------------
# nuts3_autocorr.R 
# Autor: Chris Reudenbach, creuden@gmail.com
# Urheberrecht: Chris Reudenbach 2020 GPL (>= 3)
#
# Beschreibung: Skript berechnet unterschiedliche Autokorrelationen aus den Kreisdaten
#  
#--------------------
##- Laden der Kreisdaten
#--------------------

# Aus der Sitzung Eins werden die gesäuberten Kreisdaten von github geladen und eingelesen

download(url ="https://raw.githubusercontent.com/gisma-courses/r-spatial-econometry-basics/master/docs/assets/data/nuts3_kreise.rds",     destfile = "nuts3_kreise.rds")

# Einlesen der nuts3_kreise Daten
nuts3_kreise = readRDS("nuts3_kreise.rds")

OLS Modell reloaded

Der übliche Ansatz besteht darin, die räumliche Abhängigkeit der Daten zu ignorieren und einfach eine OLS-Regression (ordinary least squares) durchzuführen.

# für die Reproduzierbarkeit der Ergebnisse muss ein beliebiger `seed` gesetzt werden
set.seed(0) 

# lineares Modell Anteil Hochschulabschluss / ANteil Baugewerbe
lm_um = lm(Universitaeten.Mittel ~ Beschaeftigte, data=nuts3_kreise)
summary(lm_um)

## 
## Call:
## lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data = nuts3_kreise)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -341649  -40552   -7942   16099  856057 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -5.839e+04  7.579e+03  -7.704 1.06e-13 ***
## Beschaeftigte  1.718e+00  6.566e-02  26.167  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 120900 on 398 degrees of freedom
## Multiple R-squared:  0.6324,	Adjusted R-squared:  0.6315 
## F-statistic: 684.7 on 1 and 398 DF,  p-value: < 2.2e-16

Räumliche Gewichtungsmatrix reloaded

Wir machen uns die Inhalte aus Sitzung 2 zu Nutze und berechnen eine (beliebige) räumliche Gewichtungsmatrix:

# für die Reproduzierbarkeit der Ergebnisse muss ein beliebiger `seed` gesetzt werden
set.seed(0) 

##Berechnung einer distanzbasiereten Nachbarschaft
# extrahiere die Flächenschwerpunkte der Kreise
coords <- coordinates(as(nuts3_kreise,"Spatial"))
# berechne alle Distanzen für die Flächenschwerpunkte der Kreise
knn2nb = knn2nb(knearneigh(coords))
# erzeuge die Kreisdistanzen
kreise_dist <- unlist(nbdists(knn2nb, coords))
# extrahiere die namen der Kreise
rn <- row.names(nuts3_kreise)
# berechne die Nachbarschaften und Gewichte für alle Kreise < Median = summary(kreise_dist)[4]
nachbarschaft_1st <- dnearneigh(coords, 0, summary(kreise_dist)[4], row.names=rn)
m_nuts3_kreise_qd =   nb2mat(nachbarschaft_1st, style='W', zero.policy = TRUE)
nuts3_gewicht <- mat2listw(as.matrix(m_nuts3_kreise_qd))

Lagrange-Multiplikator-Test

Der Moran I weißt auf räumliche Autokorrelation hin gibt uns aber keinen Hinweis zur Auswahl alternativer Modelle. Hier bietet der Lagrange-Multiplikator-Test (LM) einen Hinweis auf die zu bevorzugende Variante. Er bietet als Alternativen das Vorhandensein einer räumlichen Lags und das Vorhandensein einer räumlichen Lags im Fehlerterm. Beide Tests sowie ihre robusten Formen sind in der Funktion lm.LMtests enthalten. Um sie aufzurufen, verwenden wir die Option test="all". Auch hier müssen ein Regressionsobjekt und ein räumliches listw-Objekt als Argumente übergeben werden:

LM  = lm.LMtests(lm_um,nuts3_gewicht , 999,test = "all",zero.policy = TRUE)
LM

## 
## 	Lagrange multiplier diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data =
## nuts3_kreise)
## weights: nuts3_gewicht
## 
## LMerr = 10.593, df = 1, p-value = 0.001135
## 
## 
## 	Lagrange multiplier diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data =
## nuts3_kreise)
## weights: nuts3_gewicht
## 
## LMlag = 12.935, df = 1, p-value = 0.0003225
## 
## 
## 	Lagrange multiplier diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data =
## nuts3_kreise)
## weights: nuts3_gewicht
## 
## RLMerr = 0.93194, df = 1, p-value = 0.3344
## 
## 
## 	Lagrange multiplier diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data =
## nuts3_kreise)
## weights: nuts3_gewicht
## 
## RLMlag = 3.2746, df = 1, p-value = 0.07036
## 
## 
## 	Lagrange multiplier diagnostics for spatial dependence
## 
## data:  
## model: lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data =
## nuts3_kreise)
## weights: nuts3_gewicht
## 
## SARMA = 13.867, df = 2, p-value = 0.0009745

Da sich im Ergebnis LMerr und LMlag beide statistisch signifikant von Null unterscheiden, müssen wir uns die robusten Formen ansehen. Diese robusten Pendants sind robust gegenüber dem Vorhandensein des anderen “Typs” der Autokorrelation. Die robuste Version der Tests legt nahe, dass das Lag-Modell die wahrscheinlichere Alternative ist.

SAR und SEM Modelle

Diese Gewichtungsmatrix ist eigentlich der Zugang zum räumlichen Einfluss und abhängig vom Raummodell des theoretisch erwarteten Prozesses (z.B. spillover oder Wirtschaftskraft einer Einheit,…). Um diese räumliche Gewichtung in die Modellierung mit einfließen zu lassen werden üblicherweise die zuvor im Lagrange-Multiplikator-Test getesteten Modelle verwendet.

Spatial autoregressive model (SAR) Modell

SAR-Modelle passen lineare Modelle mit mit Hilfe von räumlichen Gewichtungsmatrizen an. Dabei wird der Raum in Form der Koordinatde als räumlicher Zusamenhäng gedeutet,

# SAR Modell
spatlag = spatialreg::lagsarlm(Universitaeten.Mittel ~ Beschaeftigte, data=nuts3_kreise, listw = nuts3_gewicht,zero.policy=TRUE, tol.solve=1.0e-30)
summary(spatlag)

## 
## Call:spatialreg::lagsarlm(formula = Universitaeten.Mittel ~ Beschaeftigte, 
##     data = nuts3_kreise, listw = nuts3_gewicht, zero.policy = TRUE, 
##     tol.solve = 1e-30)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -343035.3  -40590.8   -8689.8   14684.5  850690.2 
## 
## Type: lag 
## Regions with no neighbours included:
##  2 3 4 6 9 10 11 12 13 20 23 25 29 30 31 32 33 34 35 36 37 38 41 42 43 44 48 49 50 51 52 54 55 56 57 58 59 60 63 65 66 67 71 72 73 76 77 79 84 85 88 89 97 101 102 111 112 114 119 120 121 122 123 124 133 136 139 141 142 144 145 146 147 148 149 150 151 152 153 154 155 156 158 159 162 170 171 173 176 177 178 179 180 181 183 184 186 187 188 189 190 191 192 193 194 195 196 200 201 203 206 207 208 209 210 211 212 213 215 216 217 219 220 221 222 223 231 232 234 235 238 239 251 255 261 262 263 269 270 271 273 274 278 279 280 281 288 290 291 292 295 296 297 298 300 301 302 303 304 306 307 308 322 337 338 339 341 342 343 344 345 346 347 348 351 352 354 355 356 357 358 360 361 362 365 366 367 368 369 370 371 373 375 376 377 378 381 383 384 385 386 387 388 389 390 391 394 396 398 
## Coefficients: (asymptotic standard errors) 
##                  Estimate  Std. Error z value  Pr(>|z|)
## (Intercept)   -5.3754e+04  7.5409e+03 -7.1284 1.015e-12
## Beschaeftigte  1.7294e+00  6.4750e-02 26.7088 < 2.2e-16
## 
## Rho: -0.11785, LR test value: 9.892, p-value: 0.00166
## Asymptotic standard error: 0.042967
##     z-value: -2.7427, p-value: 0.0060929
## Wald statistic: 7.5226, p-value: 0.0060929
## 
## Log likelihood: -5242.747 for lag model
## ML residual variance (sigma squared): 1.4126e+10, (sigma: 118850)
## Number of observations: 400 
## Number of parameters estimated: 4 
## AIC: 10493, (AIC for lm: 10501)
## LM test for residual autocorrelation
## test value: 0.26505, p-value: 0.60667

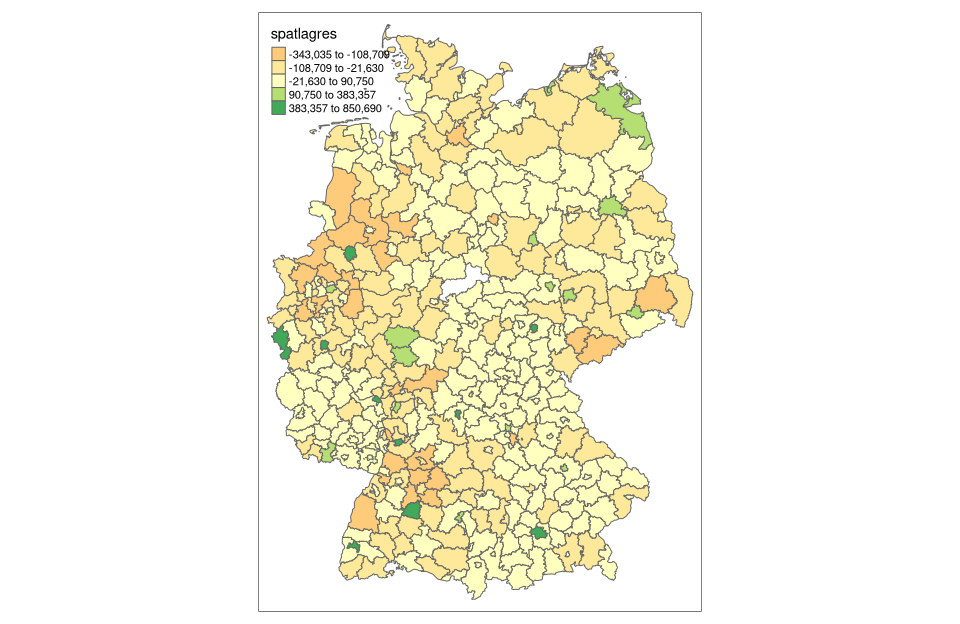
# zuweisen der Residuen in unseren nuts3_kreise Datensatz
nuts3_kreise$spatlagres = spatlag$residuals

# Moran I Test
moran.mc(nuts3_kreise$spatlagres,nuts3_gewicht , 999,zero.policy = TRUE)

## 
## 	Monte-Carlo simulation of Moran I
## 
## data:  nuts3_kreise$spatlagres 
## weights: nuts3_gewicht  
## number of simulations + 1: 1000 
## 
## statistic = 0.014836, observed rank = 732, p-value = 0.268
## alternative hypothesis: greater

# Darstellung

tm_shape(nuts3_kreise) +
  tm_borders() +
  tm_polygons(col = "spatlagres",style = "jenks" ) 

Spatial Error Modell (SEM)

Räumliche Fehlermodelle gehen davon aus, dass nur die Fehlerterme in der Regression korreliert sind. Sie spalten den Fehler in Zufallsfehler und räumlichen Fehler auf.

# SEM Modell Spatial Error Model
errspartlag = spatialreg::errorsarlm(Universitaeten.Mittel ~ Beschaeftigte, data=nuts3_kreise, listw = nuts3_gewicht,zero.policy=TRUE, tol.solve=1.0e-30)

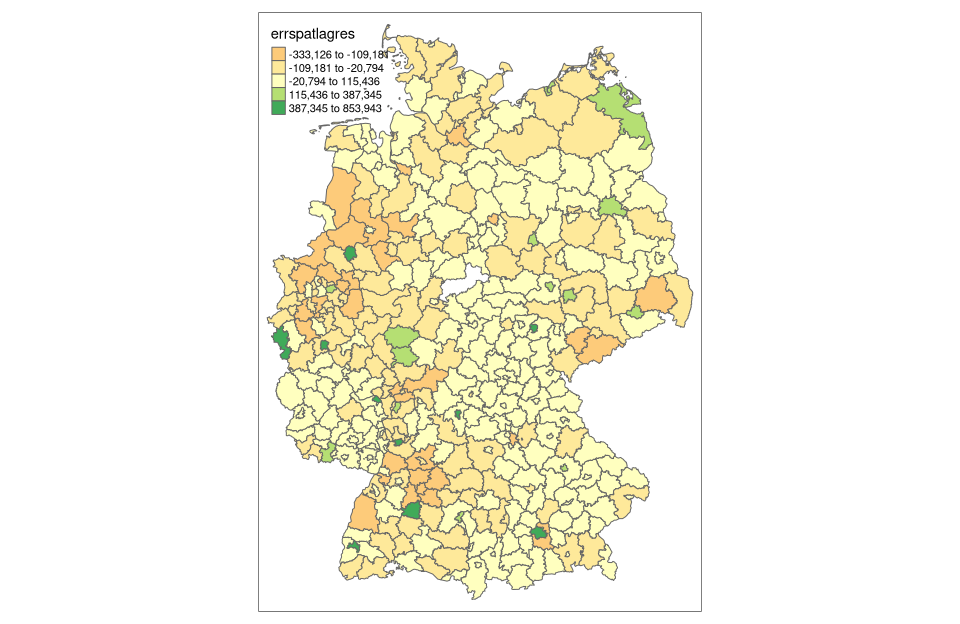
# zuweisen der Residuen in unseren nuts3_kreise Datensatz
nuts3_kreise$errspatlagres = errspartlag$residuals
moran.mc(nuts3_kreise$er,nuts3_gewicht , 999,zero.policy = TRUE)

## 
## 	Monte-Carlo simulation of Moran I
## 
## data:  nuts3_kreise$er 
## weights: nuts3_gewicht  
## number of simulations + 1: 1000 
## 
## statistic = 0.024376, observed rank = 765, p-value = 0.235
## alternative hypothesis: greater

# Darstellen der TRResiduen
tm_shape(nuts3_kreise) +
  tm_borders() +
  tm_polygons(col = "errspatlagres",style = "jenks" ) 

OLS-SEM - SAR

Wenn wir uns schließlich die likelihood Werte für das SAR-Modell und das SEM-Modell ansehen, stellen wir fest, dass wir für das SAR-Modell einen gerinfügig niedrigeren Wert erreichen als das von den LMtests favorisierte Modell. Die oben dargestellte Darstellung der Residuen zeigt immer noch eine gewisse räumliche Autokorrelation.

Wo gibt’s mehr Informationen?

Für mehr Informationen kann unter den folgenden Ressourcen nachgeschaut werden:

Spatial Regession Lab von Emily Burchfield. Sehr empfehlenswert.
Making Maps with R bietet eine sehr gelungen Einstieg in das Thema.

Download Skript

Das Skript kann unter unit05-03_sitzung.R heruntergeladen werden

Einrichten der Umgebung

rm(list=ls())
rootDIR="~/Schreibtisch/spatialstat_SoSe2020/"
## laden der benötigten libraries
# wir definieren zuerst eine liste mit den Paketnamen und 
# nutzen dann eine for  schleife die jedes element aus der  liste nimmt 
# und schaut ob es bereits installiert ist utils::installed.packages() 
# falls nicht wird es installiert 
libs= c("sf","mapview","tmap","tmaptools","spdep","ineq","cartography","spatialreg","ggplot2","usedist","raster","downloader","RColorBrewer","colorspace","viridis")
for (lib in libs){
  if(!lib %in% utils::installed.packages()){
    utils::install.packages(lib)
  }}
# nicht wundern lapply()ist eine integrierte for Schleife die alle im vector libs
# enthaltenen packages lädt indem sie den package Namen als character string an die 
# function library übergibt
invisible(lapply(libs, library, character.only = TRUE))

#---------------------------------------------------------
# nuts3_autocorr.R 
# Autor: Chris Reudenbach, creuden@gmail.com
# Urheberrecht: Chris Reudenbach 2020 GPL (>= 3)
#
# Beschreibung: Skript berechnet unterschiedliche Autokorrelationen aus den Kreisdaten
#  
#--------------------
##- Laden der Kreisdaten
#--------------------

# Aus der Sitzung Eins werden die gesäuberten Kreisdaten von github geladen und eingelesen

download(url ="https://raw.githubusercontent.com/gisma-courses/r-spatial-econometry-basics/master/docs/assets/data/nuts3_kreise.rds",     destfile = "nuts3_kreise.rds")

# Einlesen der nuts3_kreise Daten
nuts3_kreise = readRDS("nuts3_kreise.rds")

Traditionelle Regressionsvisualisierung und -Analyse

Die Visualisierung der linearen Modelle haben wir bislang vernachlässigt. neben der R-Basis Visualisierung bietet sich das überaus mächtige Paket ggplot an. Es basiert auf der gleichen Semantik der “grammar of graphics die für tmap bereits vorgestellt wurde.

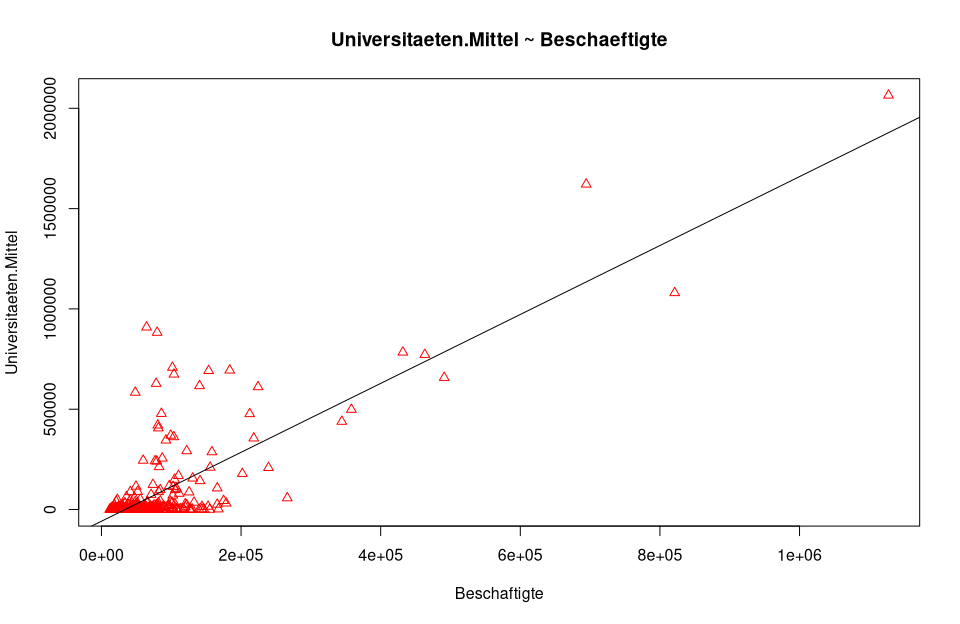
Als Beispiel nehemen wir unser OLS Modell. Die normale plot() Funktion liefert uns für die visuelle Analyse einige wichtige Grafiken die durch Enter weitergeschaltet werden können.

lm_um = lm(Universitaeten.Mittel ~ Beschaeftigte, data=nuts3_kreise)
summary(lm_um)

## 
## Call:
## lm(formula = Universitaeten.Mittel ~ Beschaeftigte, data = nuts3_kreise)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -341649  -40552   -7942   16099  856057 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -5.839e+04  7.579e+03  -7.704 1.06e-13 ***
## Beschaeftigte  1.718e+00  6.566e-02  26.167  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 120900 on 398 degrees of freedom
## Multiple R-squared:  0.6324,	Adjusted R-squared:  0.6315 
## F-statistic: 684.7 on 1 and 398 DF,  p-value: < 2.2e-16

plot(nuts3_kreise$Beschaeftigte,nuts3_kreise$Universitaeten.Mittel, pch = 2, cex = 1.0, col = "red", main = "Universitaeten.Mittel ~ Beschaeftigte", xlab = "Beschaftigte", ylab = "Universitaeten.Mittel")
# hinzufügen der Regressionsgeraden
abline(lm_um )

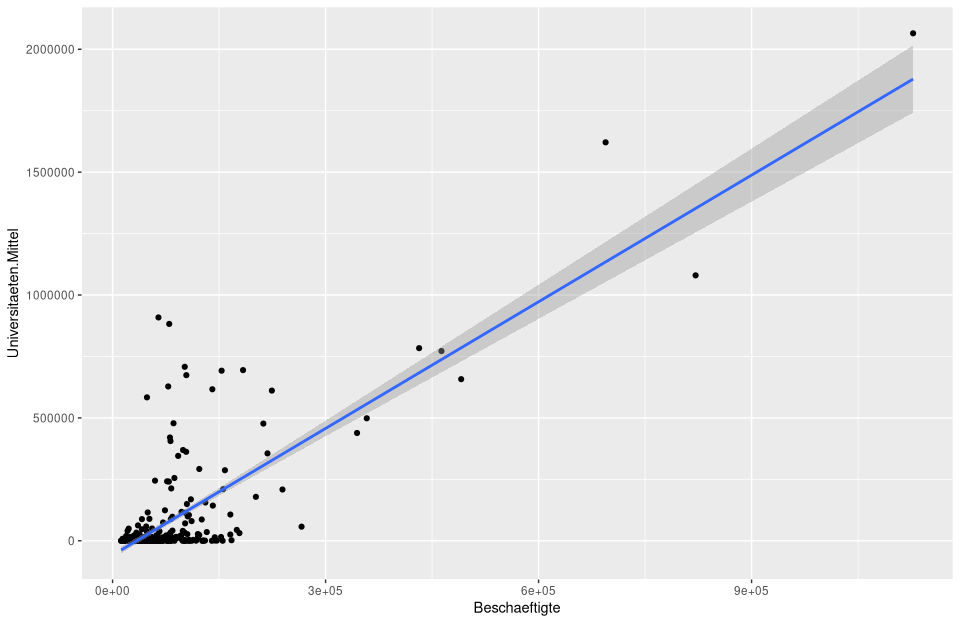
In der nachfolgenden Abbildung wird diese direkt mit ggplot berechnet und geplottet.

# berechnung und plotten des Regressionsmodells lm_um
ggplot(nuts3_kreise, aes(x = Beschaeftigte, y = Universitaeten.Mittel)) + 
  geom_point() +
  stat_smooth(method = "lm")

Natürlich können Beschriftungen und viele weitere Einstellungen manipuliert werden.

# initialisiert den Basisdatensatz
  ggplot(lm_um$model, aes_string(x = names(lm_um$model)[2], y = names(lm_um$model)[1])) + 
# für den scatterplot hinzu
    geom_point() +
# sttistische glättungfals zuviele Daten corhanden sind     
    stat_smooth(method = "lm", col = "red") +
# fügt die Überschrift mit hilfe der in lm_um gespeicherten Modelldaten hinzu
    labs(title = paste("Adj R2 = ",signif(summary(lm_um)$adj.r.squared, 5),
                       "Intercept =",signif(lm_um$coef[[1]],5 ),
                       " Slope =",signif(lm_um$coef[[2]], 5),
                       " P =",signif(summary(lm_um)$coef[2,4], 5)))

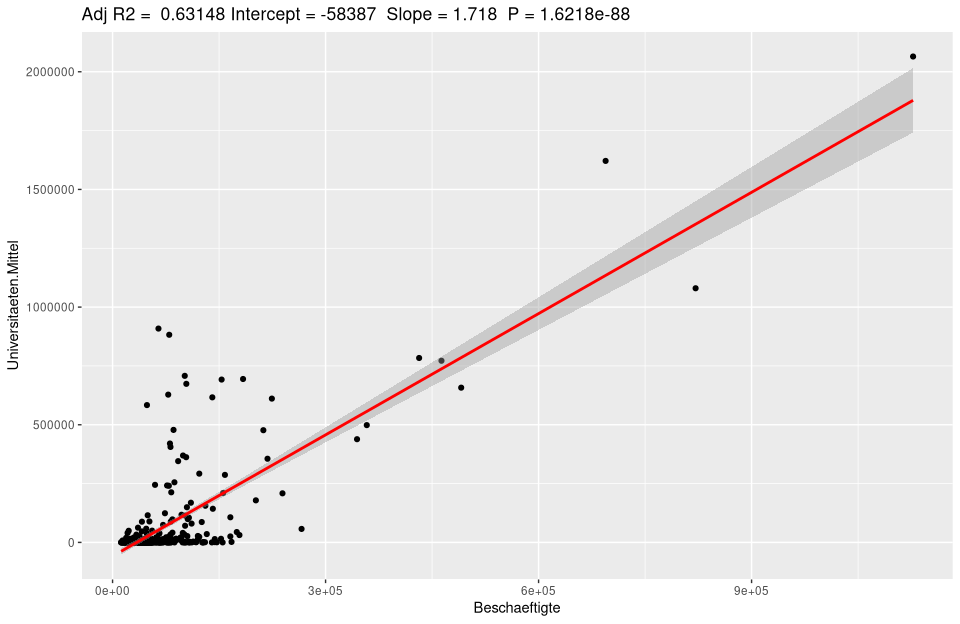
Zur Automatisierung kann es als Funktion geschrieben sehr einfach für beliebige Modelle genutzt werden.

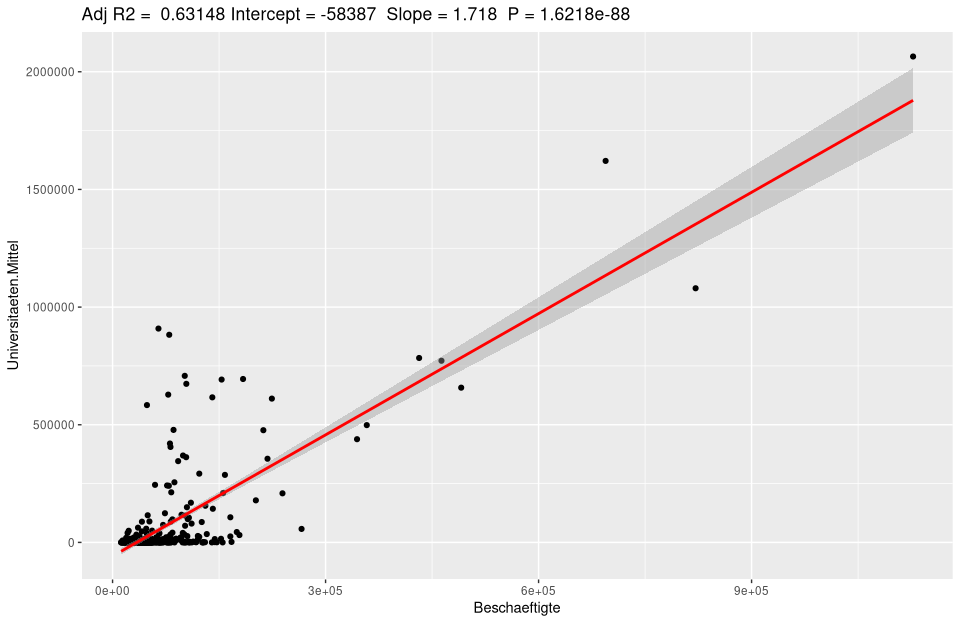
ggplotRegression <- function (fit,method="lm") {

ggplot(fit$model, aes_string(x = names(fit$model)[2], y = names(fit$model)[1])) + 
  geom_point() +
  stat_smooth(method = method, col = "red") +
  labs(title = paste("Adj R2 = ",signif(summary(fit)$adj.r.squared, 5),
                     "Intercept =",signif(fit$coef[[1]],5 ),
                     " Slope =",signif(fit$coef[[2]], 5),
                     " P =",signif(summary(fit)$coef[2,4], 5)))
}

ggplotRegression(lm(Universitaeten.Mittel ~ Beschaeftigte, data=nuts3_kreise))

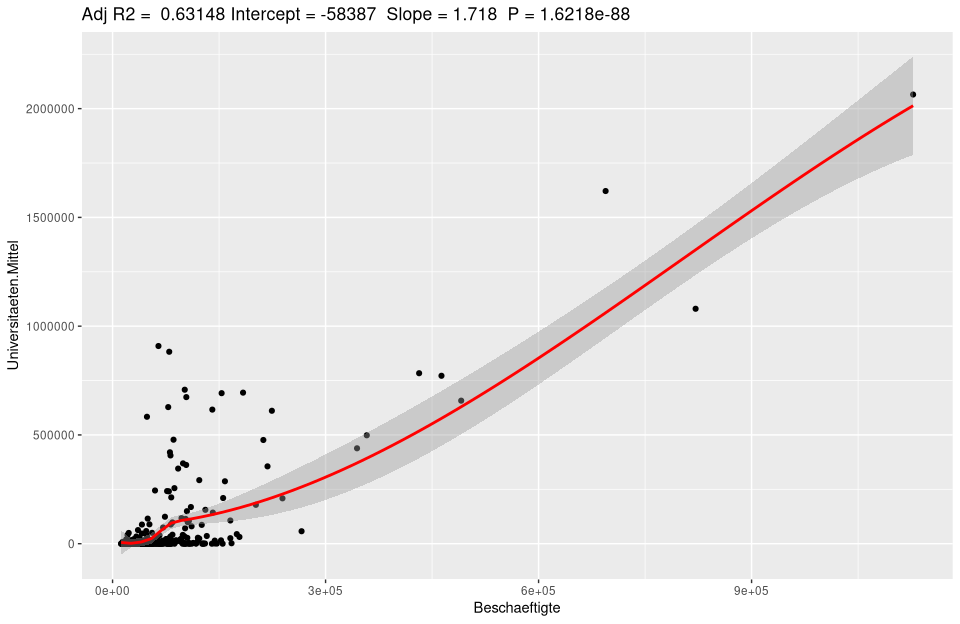
# loess model (Locally Weighted Scatterplot Smoothing)
ggplotRegression(lm(Universitaeten.Mittel ~ Beschaeftigte, data=nuts3_kreise),method = "loess")

Regressionsanalyse mit ggplot

Zur Analyse eines Regressionmodell gibt es einen typischen Ablauf. Neben den einfachen gezeigten Plots sind analytische Plots sehr hilfreich. Plotten wir unser lm_um Modell erhalten wir die folgenden 4 Abbildungen:

par(mfrow = c(2, 2))  
plot(lm_um)  

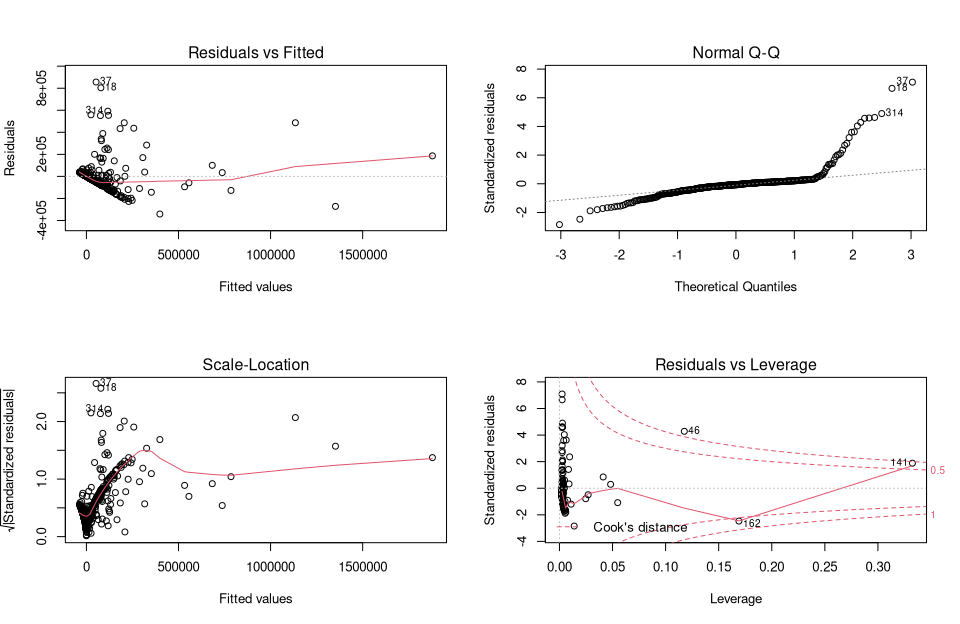
par(mfrow = c(1, 1))  

Sie stellen eine traditionelle Methode dar, um Residuen zu interpretieren und visuell zu analysieren, ob es Probleme mit dem Modell geben könnte.

Abbildung 1 (Residuals vs fitted) zeigt, ob die Residuen nichtlineare Muster aufweisen. Es könnte eine nicht-lineare Beziehung zwischen Prädiktorvariablen und einer Ergebnisvariablen bestehen, und das Muster könnte in dieser Darstellung auftauchen, wenn das Modell die nicht-lineare Beziehung nicht erfasst. Abbildung 2 (Normal Q-Q) zeigt, ob die Residuen normal verteilt sind. Folgen die Residuen einer geraden Linie oder weichen sie stark ab? Abbildung 3 (Scale Locattion) zeigt ob die Residuen gleichmäßig über die Bereiche der Prädiktoren verteilt sind. Auf diese Weise kann die Annahme gleicher Varianz (Homoskedastizität) überprüft werden. Es sollte eine horizontale Linie mit gleichmäßig (zufällig) verteilten Punkten sein. Abbildung 4 (Residuals vs Leverage) Dieser Plot hilft uns, einflussreiche Aussreißer existieren. Als Faustregel werden Randwerte in der oberen rechten Ecke oder in der unteren rechten Ecke betrachtet. Wichtig sind Ausreißer außerhalb der Cook’schen Distanz. Wenn wir diese Fälle ausschließen, werden die Regressionsergebnisse verändert.

Diese übliche Vorgehensweise kann seh relegant durch ggplot erweitert werden. Dabei folgen wir wieder dem üblichen Ansatz:

1 Anpassung eines Regressionsmodells zur Vorhersage der Variablen (Y). 2 Ermittlung von Vorhersage- und Residualwerten, die mit jeder Beobachtung auf (Y) verbunden sind. 3 Visualisierung der tatsächlichen und vorhergesagten Werte von (Y) 4 Analyse der Residuen, um eine visuelle Interpretation zu ermöglichen (z.B. rote Farbe, wenn die Residuen sehr hoch sind), um Punkte herauszustellen, die vom Modell schlecht vorhergesagt werden.

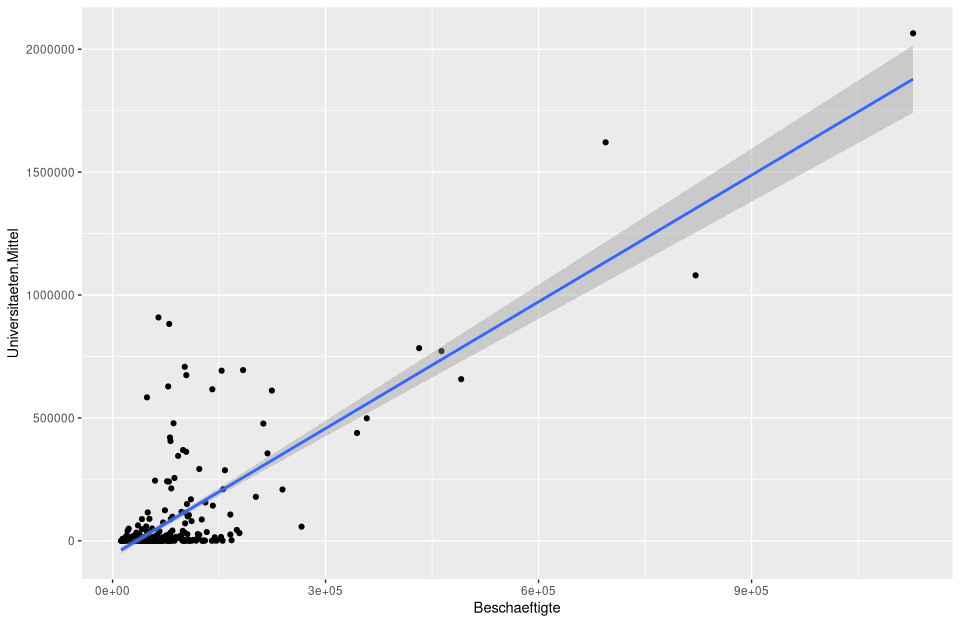
# 1) Standrd ggplot des Regressionsmodells
ggplot(nuts3_kreise, aes(x = Beschaeftigte, y = Universitaeten.Mittel)) + 
  geom_point() +
  stat_smooth(method = "lm")

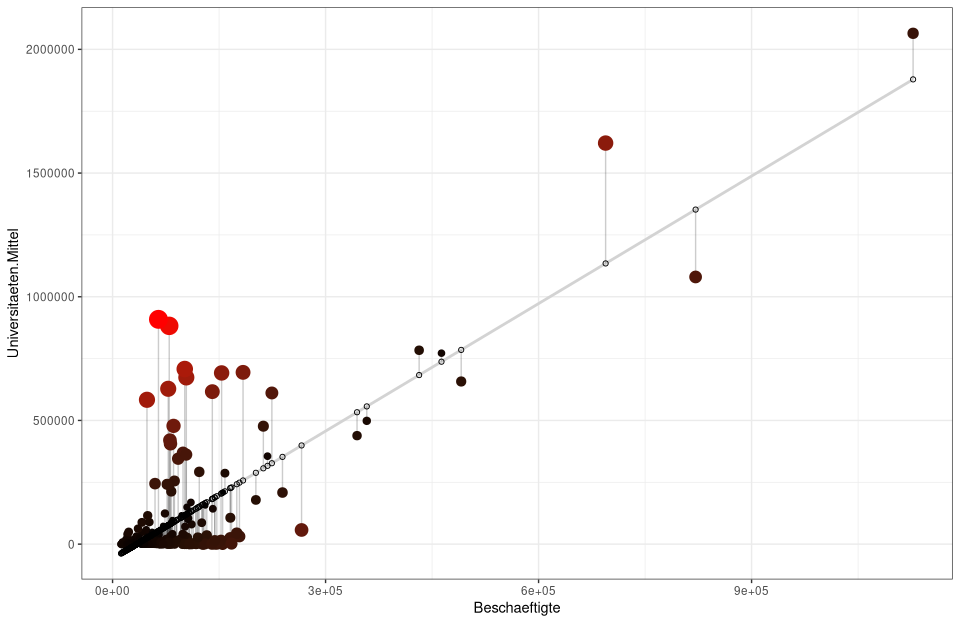
# 2) Zuweisung der Vorhersage- und Residualwerte ins nuts3_kreise Objekt
nuts3_kreise$predicted <- predict(lm_um)
nuts3_kreise$residuals <- residuals(lm_um)

# Wiederholung von 1) nur wird hier das Konfidenzintervall ausgeblendet se=FALSE, und als Farbe für die Gereade lightgrey gesetzt
# geom_segment zieht Linien  zwischen den Vorhersagewerten und Residuen während alpha die Linien transparent macht
ggplot(nuts3_kreise, aes(x = Beschaeftigte, y = Universitaeten.Mittel)) +
  geom_smooth(method = "lm", se = FALSE, color = "lightgrey") +
  geom_segment(aes(xend = Beschaeftigte, yend = predicted), alpha = .2) +

# Hier werden die Größen und Farben der Residuen erzeugt
  geom_point(aes(color = abs(residuals), size = abs(residuals))) + 
  scale_color_continuous(low = "black", high = "red") +
  guides(color = FALSE, size = FALSE) +  
  geom_point(aes(y = predicted), shape = 1) +
  theme_bw()

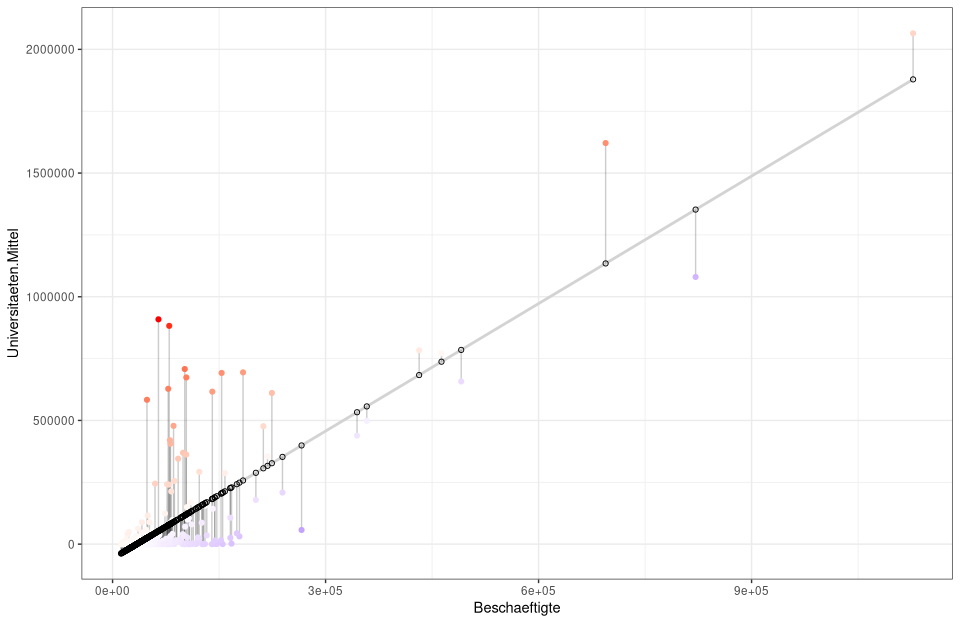
# alternativ mit Farben und ohne Größen
ggplot(nuts3_kreise, aes(x = Beschaeftigte, y = Universitaeten.Mittel)) +
  geom_smooth(method = "lm", se = FALSE, color = "lightgrey") +
  geom_segment(aes(xend = Beschaeftigte, yend = predicted), alpha = .2) +
  geom_point(aes(color = residuals)) +
  scale_color_gradient2(low = "blue", mid = "white", high = "red") +  
  guides(color = FALSE) +
  geom_point(aes(y = predicted), shape = 1) +
  theme_bw()

Farbpaletten in R

Die Farbzuweisung in Karten und Plots sind ein eigenes und durchaus komplexes Kapitel in R. Das Grundkonzept ist einfach es werden sogenannte R-Farbpaletten zum Ändern der Standardfarben genutzt. Dies gilt gleichermassen für Diagramme mit ggplot oder den R-Basis-Plotfunktionen oder auch Karten mit tmap

Die vielleicht wichtigsten Farbpalletten sind in verschiedenen R-Paketen verfügbar:

Viridis-Farbskalen [viridis-Paket].
Colorbrewer-Paletten [RColorBrewer-Paket].
Graue Farbpaletten [ggplot2-Paket]
Farbpaletten für wissenschaftliche Zeitschriften [ggsci-Paket]
R Basis-Farbpaletten: Rainbow,heat.colors, cm.colors

Die viridis Pallette zeichnet sich durch ihren großen Wahrnehmungsbereich aus. Sie nutzt den zur Verfügung stehenden Farbraum so weit wie möglich aus und ist sowohl für verschiedenen Formen der Farbenblindheit als auch für die ungebiaste Aufteilung der Farben am robustesten.

library(RColorBrewer)
library(colorspace)
clrs_spec <- colorRampPalette(rev(brewer.pal(11, "Spectral")))
clrs_hcl <- function(n) {
  hcl(h = seq(230, 0, length.out = n), 
      c = 60, l = seq(10, 90, length.out = n), 
      fixup = TRUE)
  }
### function to plot a color palette
pal <- function(col, border = "transparent", ...)
{
 n <- length(col)
 plot(0, 0, type="n", xlim = c(0, 1), ylim = c(0, 1),
      axes = FALSE, xlab = "", ylab = "", ...)
 rect(0:(n-1)/n, 0, 1:n/n, 1, col = col, border = border)
}
pal(clrs_spec(100))

pal(desaturate(clrs_spec(100)))

pal(rainbow(100))

library(RColorBrewer)
display.brewer.all()

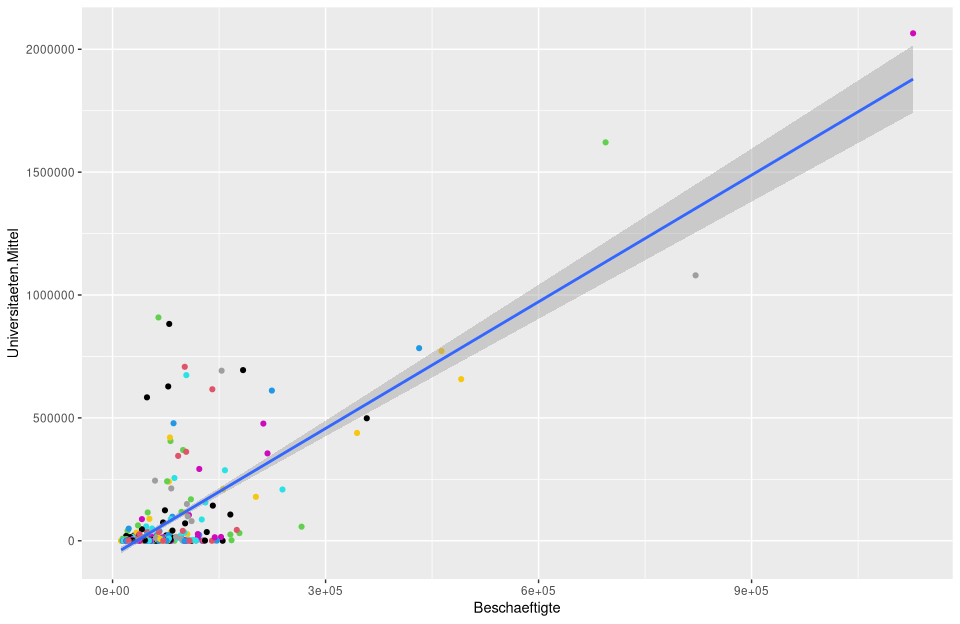
# berechnung und plotten des Regressionsmodells lm_um
ggplot(nuts3_kreise, aes(x = Beschaeftigte, y = Universitaeten.Mittel)) + 
  geom_point(color = nuts3_kreise$Beschaeftigte) +
  scale_color_viridis(option = "D")+
  stat_smooth(method = "lm")

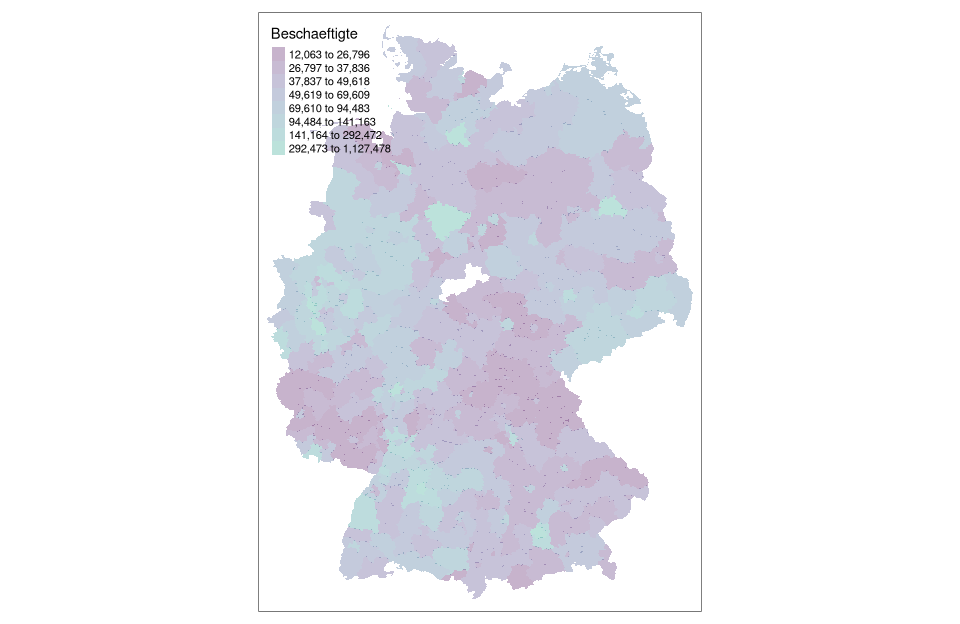
# Darstellung mit tmap Farbgebung nach em Methode mit 8 Klassen mit Hilfe der cartography::getBreaks() Funktion  
tm_shape(nuts3_kreise) + 
  tm_fill(col = "Beschaeftigte",breaks = getBreaks(nuts3_kreise$Beschaeftigte,nclass = 8,method = "em"), alpha = 0.3,palette = viridisLite::viridis(20, begin = 0, end = 0.56))

Wo gibt’s mehr Informationen?

Für mehr Informationen kann unter den folgenden Ressourcen nachgeschaut werden:

Download Skript

Das Skript kann unter unit05-05_sitzung.R heruntergeladen werden

Prüfungsaufgabenstellung

Bitte bearbeiten Sie als Projekt folgende Aufgabe:

Berechnen Sie in Bezug auf eine freigewählte Fragestellung ein lineares Modell ihrer Wahl
Untersuchen Sie das das lineare Modell auf räumliche Autokorrelation
Berechnen Sie eine für Ihre Fragestellung geeignete Nachbarschaftsmatrix und erzeugen Sie daraus eine räumliche Gewichtungsmatrix.
Modellieren Sie die Daten mit ihren Gewichtungsmatritzen mit SEM und SAR
Stellen Sie Ihre ergebnisse in einer oder mehreren Karten da
Die Abgabe erfolgt als max. 3 seitiges PDF und den verwendetn Quellcode in Ilias

Tipp: Es geht weniger um eine ausgefuchste Statistik als um einen soliden Ablauf der räumlichen Regression inklusive der kartographischen Darstellung.