Sitzung 3: Distanz, Region, räumlicher Einfluß

Geodaten sind prinzipiell wie gewöhnliche Daten zu betrachten. Durch den Raumbezug kommen allerdings die Aspekte der Skala, der Zonierung (aggregierte Flächeneinheiten), der Topologie (der Lage im Verhältnis zu anderen Entitäten), der Geometrie (Entfernung zueinander) eine Bedeutung die je nach Theorierahmen einen elementaren und zwingend zu berücksichtigenden Einfluß auf die Modellierung haben.

Als klassische oder typische Gebiete der räumlichen Statistik werden die Punktmusteranalyse, Regression und Inferenz mit räumlichen Daten betrachtet. Zur Modellierung oder Vorhersage fehlender Raumdaten werden Methoden der Geostatistik wie etwa Interpolation (z.B. Kriging) sowie AI Methoden wie Machine/Deep Learning (ML/DL) zur Vorhersage eingesetzt. Nahezu alle dieser Bereiche verwenden Daten die als Vektordatenmodell vorliegen. Vorrangig in der ML/DL Vorhersage werden in erheblichem Umfang Rasterdaten genutzt. In der Ökonometrie jedoch werden üblicherweise diskrete Geoobjekte die null-, ein- bzw. zwei-dimensionale Raumeigenschaften aufweisen.

Lernziele

Die Lernziele der zweiten Übung sind:

• Grundverständnis der räumlichen Gewichtung und Autokorrelation für die anwendung räumlicher Regressionsmodelle
• Einführun gin Distanzen, Nachbarschaften
• Berechnung unterschiedlicher Gewichtungsmatritzen
• Visualisierung der Ergebnisse

Regionalisierung oder Aggregationsräume

Auch wenn von Nutzern in der Regel Daten auf einer möglichst hoch aufgelösten Ebene bevorzugt würden (im besten Fall Einzelpersonen, Haushalte, Grundstücke, Briefkästen etc.) ist die Realität, dass es sich üblicherweise um räumlich (und zeitlich) aggregierte Daten handelt. Statt also tägliche Daten über den Cornfllakes-Kosum in jeden Haushalt verfügbar zu haben (um z.B. gezielt zu produzieren oder zu vermarkten), haben wir den Jahresmittelwert aller verkauften Zerealien in einem Bundesland. So sieht es für die meisten Daten aus, die zudem räumlich und sachlich oft unterschiedlich aggregiert sind und z.B. nationale und subnationale Einheiten (z.B. NUTS1, NUTS3, NUTS3, AMR etc.) vorliegen, die zwar formal als gleich gelten aber enorm voneinander abweichen. Die einzigen Daten die quasi-kontinuierlich erhoben werden sind Fernerkundungsdaten aus etwa aus Satellitenaufnahmen in Form von Rasterzellenwerten, die häufig in den naturwissenschftlichen Studien Verwendung finden.

Auch aus diesem Mangel betrachtet die tradionelle räumliche Ökonometrie Standorte und Entfernungen als exogen, wodurch die Modellierung der ökonomischen Variablen und etwaiger Standortentscheidungen bzw. räumlicher Abhängigkeiten nicht direkt an den Theorierahmenanknüpfbar wird, da die aggregierten Daten keinen Rückschluss auf die handlenen Subjekte zulassen. Auf diesen Handlungen basieren aber die meisten theoretischen Konzepte räumlichen ökonomischen Handelns. Der Raum wird so zur impliziten also zur abgeleiteten Größe.

Eine explizite Betrachtung des Raumes führt durch eine mikro-ökonomische Betrachtungsgrundlage auf der Basis regionaler oder sogar lokaler Daten zu charakteristisch abweichenden Merkmalen. Daraus ergen sich eine größere Realitätsnähe und größerer Informationsgehalt da durch die besser aufgelöste Datengrundlage Disaggregation und Heterogenität der zugrunde liegenden Handlungs- und Beziehungsgeflechte abbildbar werden, was eine vertiefte Analyse und Modellierung von Dynamiken ermöglicht.

So wird postuliert, dass ein räumlicher mikroökonometrischer Ansatz die Möglichkeit bietet, realistischere Modelle zu identifizieren, da in der Regel, die theoretischen Rahmen, auf Grundlage empirisch beobachteter oder behaupteter Entscheidungen der individuellen Wirtschaftsakteure abgeleitet werden. Man könnte sogar folgern, dass die bekannte Inkonsistenz zwischen mikroökonomischen Theorien und makroökonomischen in Daten abgebildeten Zusammenhängen, durch granulare, hochaufgelöste Daten zumindest gemildert werden kann.

Das Aggregationsproblem von räumlichen Daten ist ein sehr relevantes Problem bei der Analyse regionaler Daten. Räumlich aggregierte Daten basieren auf willkürlichen Definitionen der räumlichen Beobachtungseinheiten und führen so systematisch zu statistischer Verzerrung. Dieses Problem wird als modifizierbares Flächeneinheitenproblem oder MAUP bezeichnet ¹. Das MAUP wirkt sowohl als Skalenproblem, (Unbestimmtheit der Statistik hinsichtlich des Aggregationsniveaus) als auch als Aggregationsproblem (Unbestimmtheit hinsichtlich des Aggregationskriteriums). Der wohl wichtigste Effekt ist, dass die Schätzer von Regressionsparametern, bei Verwendung aggregierter statt individueller Daten, eine größere Varianz aufweisen. Das kann in erheblichem Maße zu falschen inferentiellen Schlussfolgerungen und zur Akzeptanz von ungültigen Modellen führen. So impliziert eine (fälschlicherweise angenommene) positive räumliche Korrelation eine Aggregation zwischen ähnlichen Werten, wodurch die Variabilität erhalten bleibt, während eine negative räumliche Korrelation eine Aggregation zwischen sehr unterschiedlichen Werten impliziert. Im Rahmen der räumlichen Statistik wirft das Fragen der räumlichen Autokorrelation bzw. Inhomogenität auf. Also letztlich Fragen welche Raumkonstruktion, auf welcher Skala einen Einfluss auf die Fragestellung hat.

Bei der visuellen Exploration aber auch bei der statistischen Analyse ist es von erheblichem Einfluss wie die Gebiete zur Aggregation der Daten geschnitten sind. Da wie bereits gesagt, dieser Zusammenhang willkürlich (auch oft historisch oder politisch begründet) ist, sind die Muster, die wir sehen äußerst subjektiv. Sowohl das MAUP als auch die ökologische Inferenz (Ecological Inference) also der Effekt von höheren Einheiten auf niedrigere zu schließen sind grundsätzliches methodisches Problem der räumlichen Regressionstatisik.

Distanz

Als Distanz wird die Entfernung von zwei Positionen bezeichnet. Sie kann zunächst einmal als ein zentrales Konzept der Geographie angenommen werden. Erinnern sie sich an Waldo Toblers ersten Satz zur Geographie², dass alles mit allem anderen verwandt ist, aber nahe Dinge mehr verwandt sind als ferne Dinge. Die Entfernung ist scheinbar sehr einfach zu bestimmen. Natürlich betrachten wir im einfachsten Fall Distanz als die Entfernung auf eine isometrischen und isomorhpen Fläche mittels der Luftlinie (euklidische Distanz). Zentrales Problem ist das diese Betrachtungsweise häufig, wenn noicht sogar in der Regel unzutreffend ist. Es gibt nicht nur (nationale) Grenzen, Gebirge oder beliebige andere Hindernisse, die Entfernung zwischen A und B kann auch asymmetrisch sein (bergab geht’s einfacher und schneller als bergauf). Das heißt Distanzen können auch über z.B. Distanzkosten gewichtet werden.

Üblicherweise werden Distanzen in einer “Distanzmatrix” dargestellt. Eine solche Matrix enthält als Spaltenüberschriften und als Zeilenbeschriftung die Kennung von jedem berechneten Ort. Im jedem Feld wird die Entfernung eingetragen. Für kartesische Koordinaten erfolgt dies einfach über den Satz des Pythagoras.

Erzeugen einer Distanz-Matrix

Einrichten der Arbeitsumgebung

# rootDIR enthält nur den Dateipfad, 
# die Tilde ~ steht dabei für das Nutzer-Home-Verzeichnis unter Windows 
# üblicherweise Nutzer/Dokumente
# path.expand() erweitert den relativen Dateipfad 
# !dir.exists() überprüft ob der Pfad bereits existiert damit er falls nein angelegt werden kann
rootDIR=path.expand("~/Desktop/lehre/MHG_2021/sitzung2/")
if (!dir.exists(rootDIR)) dir.create(path.expand(rootDIR))
setwd(rootDIR)

# --- Schritt 2 Download und Vorbereitung der Geometriedaten
# Schalter auswahl = "NUTS"
auswahl = "NUTS"
source(paste("../skript_sitzung_2_0.R"))

auswahl = "bertel"
source(paste("../skript_sitzung_2_0.R"))

## laden der zusätzlich zu den bereits in skript_sitzung_2_0.R geladenen Paketen
libs= c("spdep","spatialreg","ineq","rnaturalearth",  "tidygeocoder","usedist","raster","kableExtra")
for (lib in libs){
  if(!lib %in% utils::installed.packages()){
    utils::install.packages(lib)
  }}
invisible(lapply(libs, library, character.only = TRUE))


# einlesen der nuts3_kreise 
nuts3_kreise = nuts3_3035

# Erzeugen einer Hessen Geometrie für die Gemeinden
gemeinden_hessen_sf_3035 = gemeinden_sf_3035 %>% filter(SN_L=="06")

# merge der Gemeindegeometrien mit den aktuellen Datentabellen über die Spalte GEN
Bertel_HESSEN= right_join(gemeinden_hessen_sf_3035 , gemeinde_tab_all)
Kriftel_9000 = st_intersects(st_buffer(st_centroid((Bertel_HESSEN[Bertel_HESSEN$GEN=="Kriftel",])), 9000),Bertel_HESSEN)
mapview(Bertel_HESSEN[Kriftel_9000[[1]],])
Kriftel=Bertel_HESSEN[Kriftel_9000[[1]],]

Erzeugen von 10 georeferenzierten Positionen

Wir nutzen für die geroreferenzierten Positionen von 10 deutschen Städten für die Berechnung einer Distanzmatrix. Wenn die Positionen in Länge/Breite angegeben sind ist die Distanzberechnung etwas aufwendiger. In diesem Fall können wir die Funktion pointDistance aus dem raster Paket verwenden (allerdings nur wenn das Koordinatensystem korrekt angegeben wird). Eleganter ist jedoch die Konvertierung von Punktdaten in ein Geodatenformat z.B. als sf Objekt.

Zur direkten Überprüfung ob die Punkte richtig geokodiert sind eignet sich nach Erzeugung des Punkte-Objekts die Funktion mapview hervorragend. Zunächst erzeugen wir uns eine typische Punktmatrix in Form von Städten (auch als Übung um zu zeigen wie einfach solche Daten erzeugbar sind).

# Erzeugen von beliebigen Raumkoordinaten 
# mit Hilfe von tidygeocoder::osm und sf
# Städteliste
staedte=c("München","Berlin","Hamburg","Köln","Bonn","Hannover","Nürnberg","Stuttgart","Freiburg","Marburg")

# Abfragen der Geokoordinaten der Städte mit eine lapply Schleife
# 1) die Stadliste wird in die apply Schleife (eine optimierte for-Schleife) eingelesen
# 2) für jeden Namen (X) in der Liste wird mit geo() die
# Koordinate ermittelt $lat $long und in einen sf-Punkt Objekt mit (crs = 4326) konvertiert
# 3)Anfügen des Namens an das Koordinatenpaar
# 4) rbind()fügt die einzlnen listen zu einer MAtrix zusammen
geo_coord_city = do.call("rbind", lapply(staedte, function(x){
  p = st_sfc(st_point(c(geo(x,method = "osm")$long,geo(x,method = "osm")$lat)), crs = 4326)
  st_sf(name = x,p)
}))
saveRDS(geo_coord_city,"geo_coord_city.rds")
# visualize with mapview
mapview(geo_coord_city,  color='red',legend = FALSE)

Full-Screen Version der Karte

Abbildung 04-02-05: Webkarte mit den erzeugten Punktdaten. In diesem Falle zehn nicht ganz zufällige Städte Deutschlands Dann berechnen wir die Vogelflugdistanzen

Distanzberechnung von Geokoordinaten

Die Berechnung der Distanzen zwischen den 10 Städten, bzw. die korrekte Nutzung der erzeugten Punktdaten, greift einigermaßen tief in Geodaten-Verarbeitung ein: In Kürze, die Punkte liegen als geographische Koordinaten, also als unprojizierte Längen und Breitengrade auf Grundlage des WGS84 Datum vor. Auf einem Ellipsoid ist es deutlich aufwendiger (bzw. fehlerträchtiger) Entfernungen zu rechnen als in in einem projizierten (also kartesischen) Koordinatensystem. Daher müssen diese Daten geodätisch korrekt behandelt werden was kein Hexenwerk ist aber sorgfältig berücksichtigt werden muss.

Wir transformieren zunächst den Datensatz in das für Deutschland amtlich gültige Referenzsystem für Deutschland nämlich ETRS89/UTM. Im nachstehenden Beispiel nutzen wir die EPSG Konvention. Für das zuvor genannte System ist das der EPSG-Code 25832. Techsnisch nutzen wir die st_transform() Funktion des sf Pakets.

staedte=c("München","Berlin","Hamburg","Köln","Bonn","Hannover","Nürnberg","Stuttgart","Freiburg","Marburg")

# Zuerst projizieren wir den Datensatz auf ETRS89/UTM
proj_coord_city = st_transform(geo_coord_city, crs = 25832)

# nun berechnen wir die Distanzen
city_distanz = dist(st_coordinates(proj_coord_city))
# mit Hilfe von dist_setNames können wir die Namen der distanzmatrix zuweisen
dist_setNames(city_distanz, staedte)

##            München   Berlin  Hamburg     Köln     Bonn Hannover Nürnberg
## Berlin    504156.6                                                      
## Hamburg   611337.7 253841.6                                             
## Köln      456511.6 477393.1 356810.5                                    
## Bonn      434329.5 478145.8 370325.9  24607.7                           
## Hannover  489061.8 248686.4 131348.9 249893.3 258162.1                  
## Nürnberg  150928.4 377495.0 460900.6 337014.5 318118.3 338167.6         
## Stuttgart 190926.8 511243.2 533104.9 288316.8 264173.9 401815.7 157508.4
## Freiburg  278029.8 639022.5 635366.9 333440.4 309440.8 505124.9 287407.8
## Marburg   359924.1 371191.0 315365.1 128538.4 118421.0 186154.7 223271.1
##           Stuttgart Freiburg
## Berlin                      
## Hamburg                     
## Köln                        
## Bonn                        
## Hannover                    
## Nürnberg                    
## Stuttgart                   
## Freiburg   131404.0         
## Marburg    227925.4 320161.6

round(city_distanz,0)

##         1      2      3      4      5      6      7      8      9
## 2  504157                                                        
## 3  611338 253842                                                 
## 4  456512 477393 356811                                          
## 5  434330 478146 370326  24608                                   
## 6  489062 248686 131349 249893 258162                            
## 7  150928 377495 460901 337014 318118 338168                     
## 8  190927 511243 533105 288317 264174 401816 157508              
## 9  278030 639023 635367 333440 309441 505125 287408 131404       
## 10 359924 371191 315365 128538 118421 186155 223271 227925 320162

Wir erzeugen aus der Distanz-Matrix class = dist eine normale R-Matrix. Leider müssen dann die Namen wieder zugewiesen werden.

# make a full matrix an
city_distanz <- as.matrix(city_distanz)
rownames(city_distanz)=staedte
colnames(city_distanz)=staedte

Räumlicher Einfluss

Die beiden Aspekte zuvor haben die räumlichen Verhältnisse in Form von Raumabgrenzung und Distanz beschrieben. In der räumlichen Analyse ist es jedoch von zentraler Bedeutung den räumlichen Einfluss dieser Merkmale in Bezug auf die Wirksamkeit auf ein Modell zu schätzen bzw. zu messen. Dabei ist das generelle Problem, dass der räumliche Einfluss sehr komplex ist und faktisch nie zureichend ermittelt werden kann. Wie nicht anders zu erwarten gibt es daher eininge Ansätze ihn zumindest zureichend zu schätzen.

Die wichtigsten Kategorien sind: (1) prozessorientiert (funktional) durchzuführen (der oberliegende Teil eines Baches fließt in den unterliegenden) bzw. (2) datengetrieben dann wird mit statistischen Verfahren die räumliche Autokorrelation ermittelt. Für den datengetriebnen Ansatz ist dieser Einfluss in der Regel eine Funktion der Nachbarschaft oder der (inversen) Entfernung. Um damit in statistischen Modellen arbeiten zu können werden diese Nachbarschaftskonzepte als räumliche Gewichtungsmatrix ausgedrückt.

Zum Beispiel kann der räumliche Einfluss von Flächeneinheiten (NUTS3/Polygonen) aufeinander (z.B, NUTS3 Verwaltungsbezirke) so ausgedrückt werden, dass sie eine/keine gemeinsame Grenze (binär) haben, sie kann als euklidische Distanz (metrisch kontinuierlich) zwischen ihren Schwerpunkten bestimmt werden oder auch über die Länge gemeinsamer Grenzen gewichtet werden und so fort.

Nachbarschaft

Hinsichtlich des räumlichen Einflussesist die Nachbarschaft das vielleicht wichtigste Konzept (viele werden es leidvoll kennen). Höherdimensionale Geoobjekte (also ab Linie aufwärts) können als benachbart betrachtet werden wenn sie sich berühren, z.B. benachbarte Länder. Bei null-dimensionalen Objekten (Punkte) ist der gebräuchlichste Ansatz die Entfernung in Kombination mit einer minimalen/maximalen Anzahl von Punkten für die Ermittlung der Nachbarschaft zu nutzen.

Das klassische lineare Regressionsmodell geht (wie schon zuvor angesprochen) von exogenen und sphärischen Störungen aus. Betrachten wir also n-Regionen, kann eine nicht lineare (sphärische) Ausprägung der Residuen durch räumliche Autokorrelation und räumliche Heterogenität bewirken, die die optimierenden Eigenschaften der gewöhnlichen kleinsten Quadrate (OLS) verfälschend oder sogar falsch wirken.

Intuitiv wird die räumliche Korrelation als die Tatsache aufgefasst, dass nahe beieinander liegende Beobachtungen stärker korreliert sind als weit auseinander liegende (erste Satz der Geographie, Tobler, 1970). Der quantitative formale Umgang mit dieser qualitativen Behauptung erfordert jedoch die Definition des Konzepts der Nähe. In der räumlichen Ökonometrie wird Nähe als Gewichtungsmatrix oder Konnektivitätsmatrix (W-Matrix ) ausgedrückt. Von Bedeutung ist eine Schwellendistanz (=maximale Wirksamkeit), die eingeführt wird, um die Datenmenge der W-Matrix zu verringern. Technisch wird dies häufig als eine einfache binäre Matrix die zudem üblicherweise so standardisiert wird, dass die Summe in jeder Zeile eins ist, umgesetzt. Letzterer Vorgang wird Zeilennormierung genannt.

Distanzbasierte Gewichtungs-Matrix für Punkte

Anstatt den räumlichen Einfluss als binären Wert (also topologisch benachbart ja/nein) auszudrücken, kann er als kontinuierlicher Wert ausgedrückt werden. Der einfachste Ansatz ist die Verwendung des inversen Abstands (je weiter entfernt, desto niedriger der Wert).

# inverse Distanz
gewichtungs_matrix =  (1 / city_distanz)

# inverse Distanz zum Quadrat
gewichtungs_matrix_q =  (1 / city_distanz ** 2)

Wie auch die räumliche Gewichtung wird die Matrix oft zeilennormiert, das heißt dass die Summe der Gewichte für jede Zeile (Position oder Wert der Position) in der Matrix gleich ist.

# löschen der Inf Werte die durch den Selbstbezug der Punkte entestehen
gewichtungs_matrix <- as.matrix(gewichtungs_matrix)
rownames(gewichtungs_matrix)=staedte
colnames(gewichtungs_matrix)=staedte

gewichtungs_matrix[!is.finite(gewichtungs_matrix)] <- NA
zeilen_summe <- rowSums(gewichtungs_matrix,  na.rm=TRUE)
zeilen_summe

##      München       Berlin      Hamburg         Köln         Bonn     Hannover 
## 2.839529e-05 2.299421e-05 2.748176e-05 6.894169e-05 7.021031e-05 3.435182e-05 
##     Nürnberg    Stuttgart     Freiburg      Marburg 
## 3.481930e-05 3.715831e-05 2.915882e-05 4.222911e-05

Erweiterung Distanz-basierte Nachbarschaft für Flächen

Nachfolgend wird für den Mittelwert, das dritte Quartil und den Maximalwert der Distanzverteilung aller Kreis-Zentroide die Nachbarschaft bestimmt.

# Extraktion der Koordinaten aus nut3_kreise
coords <- coordinates(as(nuts3_kreise,"Spatial"))

# berechne alle Distanzen für die Flächenschwerpunkte der Kreise
knn2nb = knn2nb(knearneigh(coords))

# erzeuge die Distanzen für die LAnd-Kreise
kreise_dist <- unlist(nbdists(knn2nb, coords))
summary(kreise_dist)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    1026   11485   20205   19811   26498   56096

# Extraktion der Kreisnamen
rn <- row.names(nuts3_kreise)

# berechne die Nachbarschaften für alle Kreise < mean 3. Quartil und Max Wert
nachbarschaft_mean <- dnearneigh(coords, 0, summary(kreise_dist)[4], row.names=rn)
nachbarschaft_max <- dnearneigh(coords, 0, summary(kreise_dist)[6], row.names=rn)
nachbarschaft_thirdQ <- dnearneigh(coords, 0, summary(kreise_dist)[5], row.names=rn)

# Plotten der drei Distanzen
par(mfrow=c(1,3), las=1)
# Maxwert
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
     main=paste("Nachbarkreise näher ",round(summary(kreise_dist)[6],0) ," km", sep=""))
plot(nachbarschaft_max, lwd =1,coords, add=TRUE,col="green")

# 3. Quartil
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
     main=paste("Nachbarkreise näher ",round(summary(kreise_dist)[5],0) ," km", sep=""))
plot(nachbarschaft_thirdQ, lwd = 2, coords, add=TRUE,col="red")

# Mittelwert
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
     main=paste("Nachbarkreise näher ",round(summary(kreise_dist)[4],0) ," km", sep=""))
plot(nachbarschaft_mean, lwd =3, coords, add=TRUE,col="blue")

Abbildung 04-02-07: Distanzbasierte Nachbarschaften für die Landkreise Deutschlands, a) Nachbarschaften innerhalb der Maximaldistanz der Distanzmatrix, b) Nachbarschaften innerhalb der 3. Quartils der Distanzmatrix, c) b) Nachbarschaften innerhalb der Mittelwerts der Distanzmatrix

Binäre 4-er Nachbarschaft

Die Funktion poly2nb kann verwendet werden um binäre (=Nachbar ja/nein) Nachbarschaftslisten erzeugen. Sie dient als Grundlage einer Nachbarschaftsmatrix.

# Berchnen einer binären Nachbarschaftsliste mit der vierer Nachbarschaft "rook" (=wueen="FALSE")
rook = poly2nb(nuts3_kreise, row.names=nuts3_kreise$NUTS_NAME, queen=FALSE)

# Ableiten der Nachbarschaftsmatrix aus der zuvor erzeugten Liste
rook_ngb_matrix = nb2mat(rook, style='B', zero.policy = TRUE)

# Berechne die Anzahl der Nachbarn für jedes Gebiet
anzahl_nachbarn <- rowSums(rook_ngb_matrix)

# Berechne die Anzahl der Nachbarn als Prozentsatz
prozentzahl_nachbarn  = round(100 * table(anzahl_nachbarn) / length(anzahl_nachbarn), 1)

# Plotten der Ergebnisse
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
     main=paste("Binary neighbours", sep=""))
coords <- coordinates(as(nuts3_kreise,"Spatial"))
plot(rook, coords, col='red', lwd=2, add=TRUE)

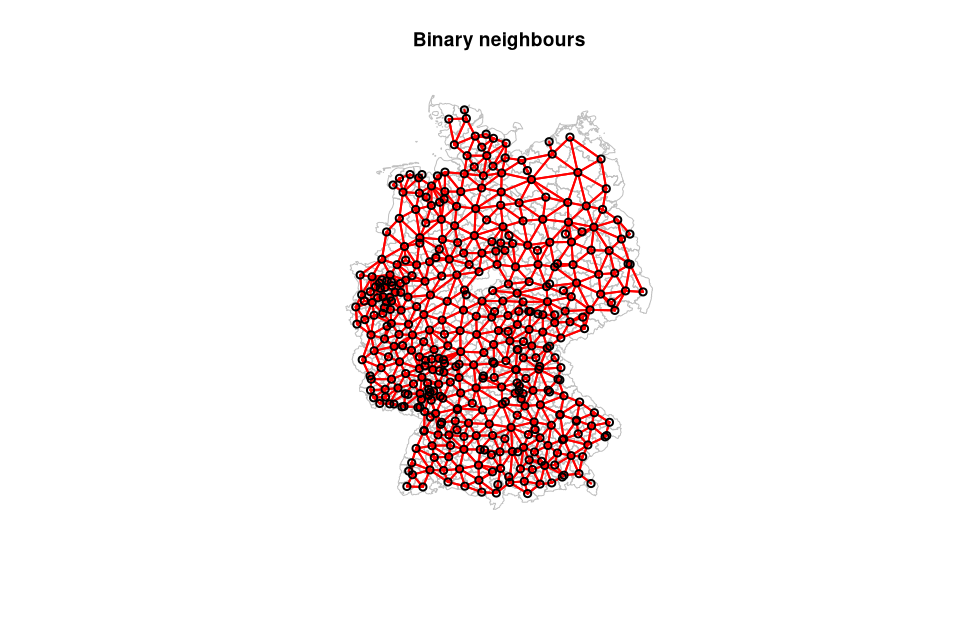
Abbildung 04-02-05: Binäre 4-er Nachbarschaft für die Landkreise Deutschlands

Nächste Nachbarn

Natürlich können auch nicht nur die vier oder acht angrenzenden Nachbarn ermittelt werden sondern beliebig viele. Nachfolgend werden exemplarisch die 3 bzw. 5 nächsten Nachbarn zu einem Kreis ausgewiesen.

rn <- row.names(nuts3_kreise)

# Berechne die 3 und 5 Nachbarschaften
kreise_dist_k3 <- knn2nb(knearneigh(coords, k=3, RANN=FALSE))
kreise_dist_k5 <- knn2nb(knearneigh(coords, k=5, RANN=FALSE))

# Plotten der Ergebnisse
par(mfrow=c(1,2),las=1)
plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
     main=paste("Drei Nachbarkreise", sep=""))

plot(kreise_dist_k3, lwd = 1, coords, add=TRUE,col="blue")

plot(st_geometry(nuts3_kreise), border="grey", reset=FALSE,
     main=paste("Fünf Nachbarkreise", sep=""))

plot(kreise_dist_k5, lwd =1, coords, add=TRUE,col="red")

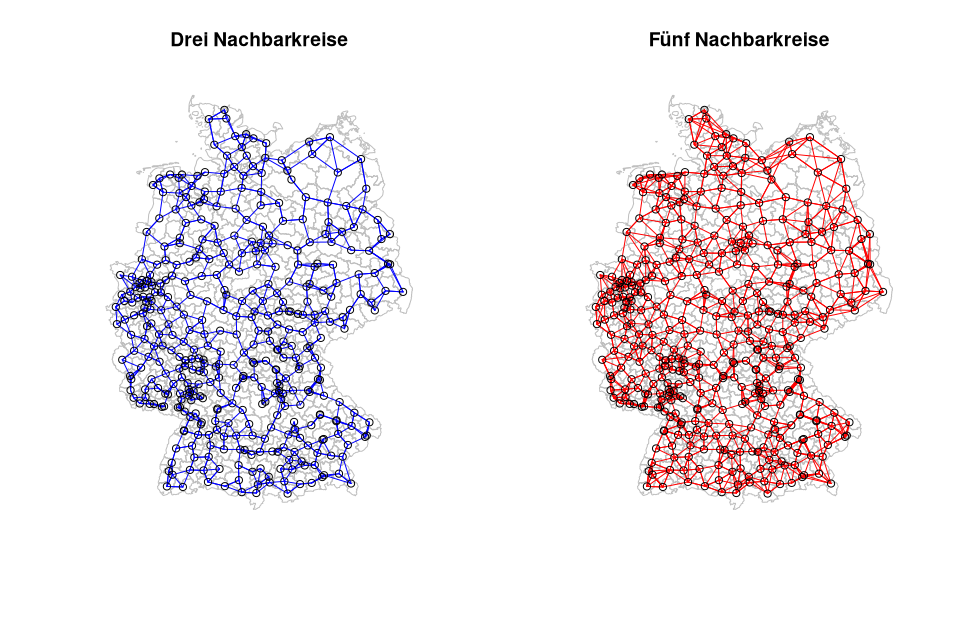
Abbildung 04-02-06:Nächste 3-er/5-er Nachbarschaft für die Landkreise Deutschlands

Räumliche Autokorrelation

Nachdem wir nun beliebige Nachbarschaften berechnen können sollten wir uns um die räumliche Autokorrelation der in diesen Nachbarschaften ausgeprägten Merkmale Gedanken machen. Die räumliche Autokorrelation die nach Tobler den Einfluß der nachbarschaftlichen Nähe beschreibt, ist komplizierter als das die zeitliche Autokorrelation. Räumliche Objekte haben in der Regel zwei Dimensionen und weisen komplexe Formen auf was zu einer mindestens zweidimensionalen Beeinflussung durch Nähe führt.

Grundsätzlich beschreiben die räumlichen Autokorrelationsmaße die Ähnlichkeit der beobachteten Werte zueinander. Räumliche Autokorrelation entstehen durch Beobachtungen und Beobachtungen und Positionen/Objekte im Raum.

Die räumliche Autokorrelation in einer Variable kann exogen (sie wird durch eine andere räumlich autokorrelierte Variable verursacht, z.B. Niederschlag) oder endogen (sie wird durch den Prozess verursacht, der im Spiel ist, z.B. die Ausbreitung einer Krankheit) sein.

Eine häufig verwendete Statistik ist Moran’s I und invers dazu Geary’s C. Binäre Daten werden mit dem Join-Count-Index getestet.

Wie bereits bekannt ist hängt der Wert von Morans I deutlich von den Annahmen ab, die in die räumliche Gewichtungsmatrix verwendet werden. Die Idee ist, eine Matrix zu konstruieren, die Ihre Annahmen über das jeweilige räumliche Phänomen passend wiedergibt. Der übliche Ansatz besteht darin, eine Gewichtung von 1 zu geben, wenn zwei Zonen Nachbarn sind falls nicht wird eine 0 vergeben. Natürlich variiert die Definition von Nachbarn (vgl. Reader räumliche Konzepte und oben). Quasi-kontinuierlich ist der Ansatz eine inverse Distanzfunktion zur Bestimmung der Gewichte zu verwenden. Auch wenn in der Praxis fast nie vorzufinden sollte die Auswahl räumlicher Gewichtungsmatritzen das betreffende Phänomen abbilden. So ist die Benachbartheit entlang von Autobahnen für Warentransporte anders zu gewichten als beispielsweise über ein Gebirge oder einen See.

Der Moran-I-Test und der Geary C Test sind übliche Verfahren für die Überprüfung räumlicher Autokorrelation. Das Geary’s-C ist invers mit Moran’s-I, aber nicht identisch. Moran’s-I ist eher ein Maß für die globale räumliche Autokorrelation, während Geary’s-C eher auf eine lokale räumliche Autokorrelation reagiert.

Berechnung der räumlichen Autokorrelation für eine binäre Vierer-Nachbarschaft

# für geneinden
h= Kriftel  %>% filter(Indikatoren=="Beschäftigungsquote (%)")
Kriftel_rook = poly2nb(t, row.names= unique(Kriftel$GEN), queen=FALSE)#
w_Kriftel_rook =  nb2listw(Kriftel_rook, style='B',zero.policy = TRUE)
m_Kriftel_rook =   nb2mat(Kriftel_rook, style='B', zero.policy = TRUE)
Kriftel_gewicht <- mat2listw(as.matrix(m_Kriftel_rook))


# lineares Modell

# Filtern der Bevölkerung und Beschäftigungsquoten

Beschäftgungsquote_2006=Kriftel  %>% filter(Indikatoren=="Beschäftigungsquote (%)")
Frauenbeschäftigungsquote_2006=Kriftel  %>% filter(Indikatoren=="Frauenbeschäftigungsquote (%)")
lm_2006 = lm(Beschäftgungsquote_2006  ~ Frauenbeschäftigungsquote_2006, data=Kriftel)
summary(lm_2006)

Call:
lm(formula = Beschaeftgungsquote_2006$`2006` ~ Frauenbeschaeftigungsquote_2006$`2006`, 
    data = Kriftel)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.5083 -1.3568 -0.6673  0.7916  5.0432 

Coefficients:
                                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)                              -9.819      6.425  -1.528    0.139    
Frauenbeschaeftigungsquote_2006$`2006`    1.288      0.135   9.542 5.57e-10 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.934 on 26 degrees of freedom
Multiple R-squared:  0.7779,	Adjusted R-squared:  0.7693 
F-statistic: 91.05 on 1 and 26 DF,  p-value: 5.573e-10


# Extraktion der Residuen
residuen_lm_2006 <- lm (lm (Beschäftgungsquote_2006$`2006` ~ Frauenbeschäftigungsquote_2006$`2006`, data=Kriftel))$resid

# Moran I test rondomisiert und nicht randomisiert
m_nr_residuen_lm_2006 = moran.test(residuen_lm_2006 , Kriftel_gewicht,randomisation=FALSE)
m_r_residuen_lm_2006  = moran.test(residuen_lm_2006 , Kriftel_gewicht,randomisation=TRUE)
summary(residuen_lm_200)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-2.5083 -1.3568 -0.6673  0.0000  0.7916  5.0432 

moran.plot (residuen_lm_2006 , Kriftel_gewicht)

Anstelle des üblichen einfachen Moran I Tests sollte eine Monte-Carlo-Simulation verwendet werden, da es eigentlich die einzige gute Methode ist festzustellen, wie wahrscheinlich die beobachteten Werte als zufällige Ziehung angesehen werden können.

moran.plot (residuen_lm_2006, nuts3_gewicht)

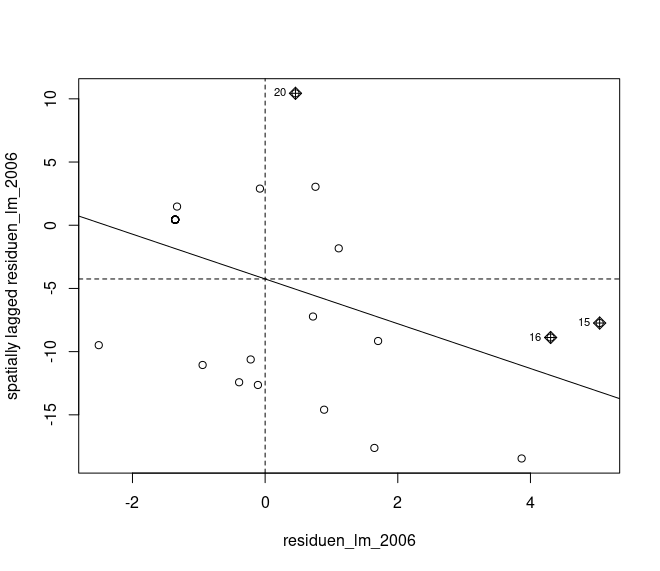
Abbildung 04-02-08: Moran-I Plot

Zusammenfassung

Es sollten die grundlegenden Konzepte der räumlichen Analyse, die die Grundlage der räumlichen Statisik bilden umrissen werden. Das sind zum einen das Konzept der der W-Matrix die Raum für räumliche Regressionsmodelle abbildet, zum Anderen der Begriff der räumlichen Autokorrelation

Download Skript

Das Skript kann unter unit05-03_bigdata.R heruntergeladen werden

Aufgabenstellung

Bitte bearbeiten Sie folgende Aufgabenstellung:

• Berechnen Sie auf der Grundlage der nuts3_kreise eine distanzbasierte Nachbarschaft mit dem maximalen Distanzmaß des ersten Quartils.
• Berechnen Sie für diese distanzbasierte Nachbarschaft eine neue Gewichtungsmatrix (analog zu nuts3_gewicht)
• Berechnen Sie mit dieser neu erstellten Gewichtungsmatrix und den residuen_uni_bau aus obigem linearen Modell mit Hilfe von Moran I die Autokorrelation mit Hilfe der Monte Carlo Variante. und vergleichen Sie die dieses Ergebnis mit dem Beispielergebnis aus dieser Übung
• Erzeugen Sie zum Abschluss eine Karte mit den Residuen des verwendenten linearen Modells. Gehen Sie hierzu analog zum tmap / mapview Beispiel vor.

Was ist sonst noch zu tun?

Versuchen Sie sich zu verdeutlichen, dass die Mehrzahl der räumlichen Regressions-Analysen und -Modelle auf den Grundannahmen dieser Übung basieren. Das heisst es kommt maßgeblich auf Ihre konzeptionellen oder theoriegeleiteten Vorstellungen an, welche Nachbarschaft, welches Nähe-Maß und somit auch, welche räumlichen Korrelationen zustande kommen. Bitte beschäftigen Sie sich mit dem Skript.

• gehen Sie die Skripte schrittweise durch. Lassen Sie es nicht von vorne bis hinten unkontrolliert durchlaufen
• gleichen Sie ihre Kenntnisse aus dem Statistikkurs mit diesen praktischen Übungen ab und identifizieren Sie was Raum-Wirskamkeiten sind.
• spielen Sie mit den Einstellungen, lesen Sie Hilfen und lernen Sie schrittweise die Handhabung von R kennen.

• lernen Sie quasi im “Vorbeigehen” wie Daten zu plotten sind oder wann Sie ein wenig Acht geben müssen wenn Sie mit Geodaten arbeiten (viele Hinweise und Erläuterungen sind in den Kommentarzeilen untergebracht).

• stellen Sie Fragen im Forum, im Kurs oder per email mit dem Betreff [gisma-courses/r-spatial-econometry-basics]

Wo gibt’s mehr Informationen?

Für R-spezifische Informationen kann unter den folgenden Ressourcen nachgeschaut werden:

• Von François Michonneau & Auriel Fournier SQL databases and R. Hier finden sich einige der Beispiele aus Block 1 und der hier gezeigten Verwendung von dplyr als Abfragesprache für die DBI Schnittstelle.
• Spatial Data Analysis von Robert Hijmans. Sehr umfangreich und empfehlenswert. Einige der Vertiefungsbeispiele basieren auf seiner Vorlesung und sind für unsere Verhältnisse angepasst.
• Der UseR! 2019 Spatial Workshop von Roger Bivand. Roger ist die absolute Referenz hinischtlich räumlicher Ökonometrie mit R. Er hat unzählige Pakete geschrieben und ebensoviel Schulungs-Material und ist unermüdlich in der Unterstützung der Community.

Zur Vertiefung von Theorie:

• Zur Theorie und anwendungsorientierter Umsetzung der Konzepte kann ein Blick in das das ausgesprochen empfehlenswerte Lehrbuch Spatial Microeconometrics nützlich sein.
• Einen guten Überblick über die Leistungsfähigkeit und Anwendungsbereiche der gängigsten Algorithmen zur Konstruktion von Nachbarschaften bietet A survey of neighborhood construction algorithms for clustering and classifying data points 2018.
• A comparison of Euclidean Distance, Travel Times, and Network Distances in Location Choice Mixture Models 2019 gibt einen guten Einblick in die theoriegeleitete Passung unterschiedlicher Distanzableitungen. Insbesondere die Resultate ab Seite 15 sind interessant.

Referenzen

1. Ariba G.: Spatial Data Configuration in the Statistical Analysis of Regional Economics and Related Problems. Kluwer, Dordrecht (1989) ↩

2. Tobler, W. R., A Computer Movie Simulating Urban Growth in the Detroit Region. In: Clark University (Hrsg.): Economic Geography, Vol. 46, Supplement: Proceedings. International Geographical Union. Commission on Quantitative Methods. Band 46, Juni 1970, S. 234–240 ↩