Kriterienverschneidung

Das Prinzip der Verschneidung („overlay“) räumlicher Daten ist konzeptionell sehr einfach. Zunächst werden zwei oder mehr thematische Informationsebenen desselben Raumausschnittes überlagert. Da es sich um die Manipulation von Geometrien handelt wird die Topologie der neuen Datenebene aufgrund dieser Überlagerung neuberechnet. Bezogen auf ein Vektordatenmodell sieht das wie folgt aus: Liegt ein betrachteter Punkt innerhalb eines Polygons, erhält er diese Information als neues Attribut. Schneiden sich zwei Linien, so wird an ihrem Schnittpunkt ein neuer Knoten eingeführt. Schneiden sich zwei Polygone, erhält die Schnittmenge eine eigene Identifikationsnummer usw.. Damit diese räumliche Datenintegration korrekt ist, müssen alle Eingangsebenen ein identisches Referenzierungssystem aufweisen. Die Integration von Informationen aus verschiedenen Quellen durch Verschneidung ist eine der bedeutendsten räumlichen Grundfunktionen eines GIS.

Boolesche Verschneidung

In einfachen Eignungsanalysen führt oft bereits die logische Kombination von wahr/falsch-Informationen zur Lösung. Angenommen, die in den Marburger Uniwald eingewanderte Wildkatze siedelt nur im Laubwald und nur in steilen Gebieten, so reichen wenige logische Überlegungen, um die geeigneten Lebensräume für die Katze zu ermitteln. Jedes dieser beiden Kriterien kann mit einer binären Informationsebene modelliert werden (Wald/Nicht-Wald und Steil/Nicht-Steil). Als potenzielle Lebensräume eignen sich nun genau die Gebiete, für die beide Kriterien zutreffen. Mit anderen Worten: Gebiete, die wahr sind für Wald UND für steil. Die Boolesche Verschneidung eignet sich v. a. bei Eignungsanalysen mit randscharfen und klar ausschliessenden Kriterien. Kann als Katzenlebensraum das Siedlungsgebiet und die landwirtschaftliche Nutzfläche zum Beginn der Analyse bereits ausgeschlossen werden, so ist das potenzielle Eignungsgebiet mit einer einfachen Booleschen Verschneidung rasch ermittelt.

Für viele Fragen ist allerdings die Einteilung der Welt in nur zwei Kategorien unbefriedigend oder besser unzureichend. So lassen sich v. a. für Kriterien der natürlichen Umwelt selten trennscharfe Grenzen angeben.

Die gewichtete Verschneidung

Für viele Fragestellungen stellt die Einteilung der Realität in die binäre Kategorie wahr oder falsch eine unzureichende Abbildung der Realität dar. Die gleichgewichtete ausschliessende Wirksamkeit der Einflussfaktoren bildet meist nicht die reale Gewichtungen von Entscheidungen ab.

So mag, wer ein neues Mobiltelefon kauft, Marke und Funktion bedeutsamer finden als Displaygröße, Preis oder Robustheit. Dieses allgemeine Prinzip der Gewichtung von Einflussfaktoren wird auch bei der Eignungsanalyse mit GIS verwendet. Der entsprechende Ansatz heißt gewichtete Verschneidung.

In vielen Raumanalysen sind bestimmte Kriterien bezogen auf die Zielsetzung um ein n-faches wichtiger als andere. Oft ist es gerade ein Anspruch an eine Standortsuche, mehrere geeignete Orte darauf hin zu vergleichen, ob und wie stark sie einer Reihe von unterschiedlich wichtigen Kriterien entsprechen. Durch das Ebenenprinzip der GI-Systeme lässt sich die Verschneidung sehr einfach um die Idee unterschiedlich wichtiger Kriterien erweitern. Jeder Themenebene wird entsprechend ihrer relativen Bedeutung gegenüber den anderen ein numerischer Gewichtsfaktor zugeordnet. Anschließend werden die derart gewichteten Informationsebenen verschnitten wie bisher. Wie die Boolesche Verschneidung ist auch die gewichtete Verschneidung grundsätzlich sowohl im Raster- als auch im Vektormodell möglich. So könnten z.B. Tourismusexperten einer Urlaubsinsel die negative Wirkung von Hotels und Bars für ein Alternativtourismuskonzept mit dem Faktor 0.1 und Quad-Trek-Routen durchs Binnenland mit dem Faktor 1 gewichten. In der Regel sollten die Wertebereiche der Eingangs-Informationsebenen normalisiert sein (also zwischen z.B. 0 und 1 skaliert). In der entstehenden Eignungsebene werden die geeigneten Räume oder Standorte durch besonders hohe Werte identifizierbar.

Katzen im Lahntal

Betrachten Sie das folgende Beispiel. Hier wird die gewichtete Verschneidung am Beispiel des Wildkatzenlebensraums im Marburger Uniwald eingeführt. Im Hinblick auf eine realistischere Modellierung der geeigneten Lebensräume verwendet das folgende Beispiel nicht mehr ausschließlich binäre Eingangsdaten wie die Boolesche Verschneidung, sondern sogenannte Ratiodaten:

Vegetationsdichte anstelle „Wald/Nicht-Wald“
Hangneigung anstelle „steil/nicht-steil“
Bevölkerungsdichte anstelle „Siedlung/Nicht-Siedlung“

Der wohl einfachste Ansatz für eine gewichtete Verschneidung bildet die gewichtete lineare Summierung im Rastermodell. Die folgenden Punkte zeigen das Standardvorgehen bei der Anwendung dieses Algorithmus:

Kriterienwahl: Der erste Schritt besteht in der Wahl der Kriterien, die den gesuchten Raum charakterisieren.
Standardisierung: Nun müssen die unterschiedlichen Messskalen der Eingangsdatensätze aufeinander abgestimmt werden. Es wenig sinnvoll, die prozentuale Hangneigung direkt mit einer Bevölkerungsdichte zu verrechnen. Deshalb weist man den Eingangsdaten völlig verschiedene Einheiten einer standardisierten numerischen Indexskala zu (beispielsweise 0–1, 0–100, 0–255). Daraus folgt, dass die Werte der resultierenden Eignungsebenen keine Einheiten mehr tragen, sondern lediglich einen numerischen Eignungsindex. Die Zuordnung der Eingangswerte auf die Indexskala kann auf verschiedene Weise erfolgen, am einfachsten ist eine lineare Zuordnung. Bei der gewichteten Verschneidung bezeichnet die Standardisierung die Übersetzung der heterogenen Eingangsdaten in eine für alle Ebenen einheitliche Skala.
Verteilung der Gewichte: Weiter erhält jede Informationsebene einen Multiplikator, ein Gewicht. Die Gewichte widerspiegeln die relative Bedeutung der Informationsebenen zueinander. Die wichtigste Ebene erhält das größte Gewicht. Die richtige Wahl der Gewichte wird in „Bestimmung der Gewichte“ behandelt.
Anwendung des Algorithmus: Beim Algorithmus der gewichteten linearen Summierung werden alle Rasterzellen einer Informationsebene mit ihrem Gewicht multipliziert und die Ebenen anschließend addiert. In der resultierenden Eignungsebene weisen die geeigneten Rasterzellen hohe, die ungeeigneten hingegen tiefe Werte auf.

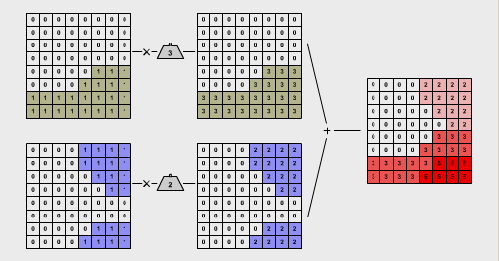
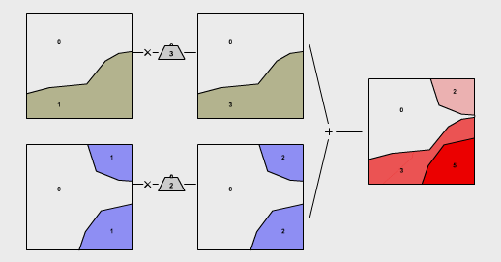
In dieser Darstellung erhielten die beiden Eignungskriterien für den Katzenlebensraum im Lahntal Gewichte entsprechend ihrer relativen Bedeutung. Die Infomationsebene „bewaldet“ wird mit dem Faktor 3 gewichtet, diejenige mit dem Kriterium „steiles Gelände“ mit dem Faktor 2. Nach der Zuweisung der Gewichte werden die beiden Ebenen addiert. Die Eignungswerte der resultierenden Informationsebene reichen von 0 (ungeeignet) bis 5 (sehr geeignet).

Methoden zur Bestimmung der Gewichte

Im Prozess der Entscheidungsfindung ist, wie bereits angeschnitten wurde, für verschiedenen Interessengruppen die einzelnen Bewertung und Bedeutung der einzelnen Kriterien unterschiedlich. Wie sollen solche Bewertungen vergleichbar gemacht werden? Genau die gleiche Frage stellt sich bei der Suche nach dem Lebensraum für den Wolf in St. Gittal. Angenommen die Experten und Expertinnen hätten sich darauf geeinigt, eine gewichtete Verschneidung für ihre Eignungsanalyse zu verwenden. Wie sollen sie nun die einzelnen Kriterien gewichten? Wie kommen die Experten darauf, dass etwa das Kriterium „Rückzugsgebiet Wald“ 1,5-mal so wichtig sein soll wie „steiles und felsiges Gelände“? Die Verteilung der Gewichte ist bei einer Eignungsanalyse mit gewichteter Verschneidung genauso wichtig wie schwierig. Diese Unit zeigt drei Methoden, wie im Dialog mit den Experten eine Gewichtung der Kriterien erfolgen kann.

Gewichtung nach Ranglisten

Am einfachsten erfolgt eine Gewichtung über eine Rangierung („ranking“) der Kriterien. Dabei kann aufsteigend oder absteigend rangiert werden. Aufsteigend bedeutet, dass das wichtigste Kriterium den Rang 1 erhält, das zweitwichtigste den Rang 2 usw. Durch eine absteigende Rangierung erhält das unwichtigste Kriterium den Rang 1, das nächst wichtigere den Rang 2 usw. Sind die Ränge einmal verteilt, können die den Rängen entsprechenden numerischen Gewichte auf verschiedene Weise abgeleitet werden.

Summierend: Bei n Kriterien erhält der Rang r das Gewicht n – r + 1.
Reziprok: Bei n Kriterien erhält der Rang r das Gewicht 1 / r, also seinen Kehrwert.
Exponentiell: Bei n Kriterien erhält der Rang r das Gewicht (n – r + 1) ^ p. Dabei ist der Exponent p ein Parameter, um die Verteilung der Gewichte zu steuern. Ist p = 0, erhalten alle Kriterien das gleiche Gewicht. Der Wert p = 1 gewichtet wie die summierende Gewichtung. Je höher p wird, desto steiler wird die Gewichtsverteilung.

Meist werden die einzelnen Gewichte um eine einfache Vergleichbarkeit zu erhalten normalisiert: Durch die Division der einzelnen Gewichte durch die Summe aller Gewichte werden die einzelnen Gewichte zu Bruchzahlen im Wertebereich 0-1 umgerechnet. Die Summe der normalisierten Gewichte beträgt 1.

Kritische Diskussion der Gewichtungsmethoden

Auch die gewichtete Verschneidung hat Schwachpunkte und weist Probleme auf. Das größte Problem bildet sicher die Zuordnung der Gewichte. Wie Sie selbst gesehen haben, beeinflussen sie das Resultat einer Eignungsanalyse erheblich. Mit welcher Rechtfertigung erhielt die Vegetationsebene im obigen Beispiel das größte Gewicht? Meist nehmen Experten und Expertinnen diese Gewichtung vor und berufen sich dabei auf Angaben in der Fachliteratur. Aber unterschiedliche Fachleute werden die Gewichtung der Kriterien je nach eigenen Interessen unterschiedlich vornehmen. So dürften Biologen, Touristiker und Jäger die Gewichtungen zur Bestimmung der geeigneten Wolfslebensräume in St. Gittal sehr unterschiedlich vornehmen. Im obigen Beispiel erfolgte die Gewichtung willkürlich. Die folgende Unit zeigt, dass es auch andere Vorgehensweisen gibt. Weiter gilt es festzuhalten, dass in vielen SDSS-Anwendungen gezielt ein experimenteller Umgang mit der Gewichtsverteilung gepflegt wird. Im Sinne von „was wäre wenn“-Szenarien kann so der Einfluss verschiedener Kriterien in einer Eignunsanalyse untersucht werden. Ein weiteres Problemfeld ist die Wahl des Evaluationsalgorithmus. Anstatt einer linearen Zuordnung der Eingangs- auf die Indexskala, wären beliebige andere Funktionen denkbar. Und anstatt die gewichteten Eingangsebenen zu summieren, könnten sie auch z. B. multipliziert oder verrechnet werden. Die Resultate einer Eignungsanalyse können selbst bei identischen Eingangsdaten und identischen Gewichten je nach Wahl des Verrechnungsmodus beträchtlich variieren. Aus diesen Gründen ist beim Einsatz der gewichteten Verschneidung stets darauf zu achten, die Entstehungsbedingungen der Resultate klar aufzuzeigen. Nur so können die Eignungskarten als das dienen, was sie wirklich sind: ein objektives Hilfsmittel zur Entscheidungsunterstützung.

Die gezeigten Methoden unterscheiden sich durch die ihnen zugrunde liegende Skala. Die Gewichtung nach Ranglisten und die Gewichtung durch Einstufungstehen weitgehnd ohne theoretische Grundlage da. Welche der Methoden zum Einsatz kommt, hängt von einer Reihe von Fragen ab: Wie genau muss die Analyse sein? Wie gross ist die Fachkompetenz und die Erfahrung der Fachleute mit gewichteter Verschneidung? Oder wie schwierig ist die Integration der Methode in ein GIS? Die grosse Gefahr beim Einsatz von Gewichtungen in der räumlichen MCE liegt in der unbedarften, unvorsichtigen oder falschen Festlegung der Gewichte. Falsche Gewichte führen zu falschen Resultaten der Eignungsanalyse und können so zu falschen Entscheidungen führen. Diese Gefahr besteht bei allen drei Methoden, da die Gewichtung letztlich immer in der Verantwortung von Fachleuten liegt.

Jede Eignungskarte oder Raumanalyse muss vollständig Transparenz darstellen wie sie aus welchen Gründen erzeugt wurde

Denken Sie mit…

Betrachten Sie erneut die Übung zur gewichteten Verschneidung.
Wie würden Sie vorhehen um eine transparente Dokumentation ihrer gewählten Gewichte vorzunehmen?
Wie würden Sie vorgehen um die Gewichte zu ermitteln?