Raum-Datenmodelle
Wir haben im Reader 01 festgestellt, dass diskrete Geoobjekte sowie multidimensionale Merkmalsausprägungen von Raumkontinua mit Hilfe von Koordinaten verortet und als Geographische Daten in Computern gespeichert werden können. Solche binären Geodaten stellen folglich die geographische Repräsentation von Wirklichkeit in GI-Systemen dar.
Die Grundlage für die Informationsreduktion bilden sogenannte Datenmodelle. Ein Datenmodell wird durch die Abstraktion von einzelnen Objekten (Entitäten) und deren Eigenschaften (Attribute) gebildet. In diesem Vorgang werden gleiche Objektarten (z. B. Flüsse, Bundesstraßen, städtische Gebiete) zusammengefasst. Da die Grundlage aller GI-Systeme auf einer räumlichen Repräsentationen beruht, muss die schon bekannte Geographische Abstraktion für ein besseres Verständnis der Datenmodellierung etwas reorganisiert und angepasst werden.

Dieses Konzept verdeutlicht allerdings nicht die konkrete digitale bzw. technische Umsetzung. Die betrachteten Geoobjekte der Echtwelt enthalten eine nach wie vor gegen unendlich strebende Fülle von Informationen. Gleiches gilt noch mehr für die Raumkontinua, die je nach Skala beliebig komplex sein können. Für die digitale Repräsentation räumlicher Merkmale, benötigen wir daher eine effiziente und einfache Methode, Informations- bzw. Datenreduktion betreiben zu können.

Die Abbildung zur Repräsentation als Raster- und Vektordatenmodell verdeutlicht diesen zentralen Aspekt der Modellierung räumlicher Daten. In der Anwendung von GIS haben sich hierfür zwei vollständig unterschiedliche Datenmodelle etabliert, die Rastermodell bzw. Vektordatenmodell genannt werden. Beide Datenmodelle sind prinzipiell sowohl für die Repräsentation von kontinuierlichen Eigenschaften, als auch von diskreten Geoobjekten verwendbar. In der Praxis werden jedoch kontinuierliche Daten gewöhnlich im Rasterdatenmodell und diskrete Daten im Vektordatenformat abgebildet. Beide Datenmodelle unterscheiden sich vorrangig in der Art der räumlichen Repräsentation ihrer Merkmale, was auch in der Abbildung deutlich wird. Bitte beachten Sie, dass die genannten Datenmodelle nicht nur für die Repräsentation zeitlich fester Merkmalsausprägungen, sondern auch für sich zeitlich verändernde Merkmale verwendet werden können.
Das Vektordatenmodell
In einem kartesischen Koordinatensystem, das zur Repräsentation einer euklidischen Geometrie notwendig ist, können aus dem Grundelement Punkt beliebig komplexe räumliche Strukturen zur Modellierung von Geoobjekten aufgebaut werden. In der Schule haben Sie solche Punkte auch als Vektoren kennengelernt und in der (Geo-)Informatik und dem topologischen Kontext der Geographie spricht man von Knoten. Wenn wir zwei Knoten im Koordinatensystem referenziert haben, können wir diese Knoten durch eine Linie verbinden, die topologisch als Kanten bezeichnet wird. Wenn nicht nur zwei Knoten durch eine Kante verbunden sind, sondern als Resultat der Verbindung von mindestens drei Knoten durch Kanten eine geschlossene Fläche entsteht, spricht man von einem Polygon bzw. topologisch von einer Masche. In GI-Systemen werden Knoten in der Regel als Punkte bezeichnet, nicht-geschlossene Verbindungen von Kanten als Linie und Maschen als Polygone.

Das Rasterdatenmodell
Anders als beim Vektordatenmodell wird bei Rasterdatenmodellen der Raum grundsätzlich mit Hilfe zwei- bzw. dreidimensionalen Objekten in beliebiger Form und Größe, aber ohne gegenseitige Überschneidung bzw. Lücken abgebildet. Die Merkmalsausprägungen werden als Zahlenwerte, die jeder Zelle zugeordnet sind, abgespeichert.
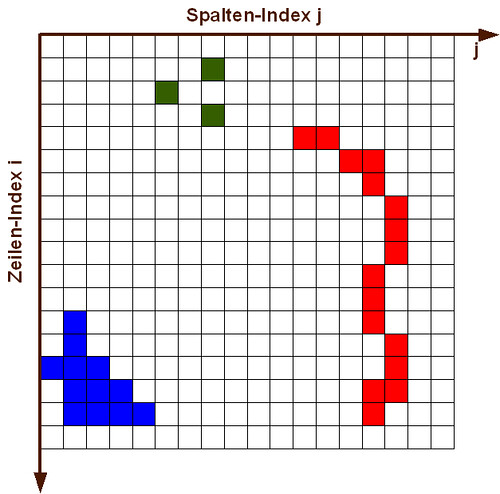
Obwohl möglich, sind Rasterdatenmodelle mit unregelmäßig geformten Zellen in der GIS-Praxis quasi nicht existent. Meist sind die Zellen in einer gleichförmigen Matrix, z.B. einem Gitter (grid) aus Zeilen (horizontal) und Spalten (vertikal) angeordnet (vgl. Abbildung Rastermodell). In der Praxis werden regelmäßige Maschen fast ausschließlich als Quadrate (gelegentlich auch als Dreiecke bzw. Sechsecke) verwendet. Diese Quadrate werden in Zusammenhang mit Rasterdaten als Rasterzelle oder Pixel (picture element) bezeichnet.

Durch Anordnung, der sich nicht überschneidenden Zellen in Zeilen und Spalten entsteht ein impliziter Raumbezug jeder Zelle. Zu beachten ist dabei, dass der Ursprung eines Rasterbildes immer in der oberen linken Ecke liegt und von dort üblicherweise mit den beiden Laufindizes i, j durchgezählt wird. Hierdurch ist jedes Pixel eindeutig identifizierbar. Auf diese Weise ist bezogen auf jedes Pixel auch ein expliziter Raumbezug vorhanden. Allerdings nutzt der theoretische explizite Raum wenig für die Verortung in einem definierten kartesischen Koordinatensystem bzw. in der Echtwelt. Diese Verortung ist sowohl für die gemeinsame Verwendung von Rasterdaten mit Vektordaten notwendig, als auch unerlässlich für die geographischen Referenzierung der Rasterzellen bezogen auf die Echtwelt. Daher werden Rasterdatenmodelle grundsätzlich auch mit einem kartesischen Koordinatensystem versehen. Dieses hat allerdings den Ursprung (wie üblich) in der unteren linken Ecke. Die Rasterzellen können also sowohl über ihren Laufindex als auch über das kartesische Koordinatensystem im Raum identifiziert werden.
Denken Sie mit…
Öffnen Sie mit Google Earth die Datei die zuvor heruntergeladene Datei Raster oder Vektor. Versuchen Sie zu identifizieren, welches Datenmodell für welche der dargestellten Information verwendet wird.
- Welche(s) Datenmodell(e) nutzt ihrer Meinung nach Google Earth?
- Lassen sich aus den am Bildschirm dargestellten Informationen nähere Eigenschaften des verwendeten Datenmodells ableiten? Wenn ja welche? Wenn nein warum nicht?
- Schalten Sie auf Vertikalsicht und entfernen Sie die Option Gelände. Zoomen Sie sich langsam bis auf 10 Meter Höhe über Grund. Was beobachten Sie?
