Projektionen - Die Vermessung der Welt
Die zentrale Aufgabe eines Koordinatensystems in Geoinformationssystemen ist die räumlich reproduzierbare Verortung diskreter und/oder kontinuierlicher Elemente geographischer Information. Über die unmittelbaren Raumdimensionen hinausgehende Eigenschaften können den Geoobjekten als Attribute zugeordnet werden. Um die Realwelt abstrahieren zu können, muss unsere GIS-Software grundlegende Methoden zur Verfügung stellen, die das geographische Datentripel Zeit, Ort und Attribut konsistent nutzbar machen.
Die aktuelle Sitzung ist für ein schrittweises Erarbeiten dieser komplexen Materie in mehrere Abschnitte gegliedert. Zunächst werden die Prinzipien der räumlichen Referenzierung (Georeferenzierung) mit Hilfe von Ortsnamen, die lineare Referenzierung und das exakte zweidimensionale Verorten in einem Katastersystem besprochen. Im Anschluss werden die wichtigsten geodätischen bzw. kartographischen Methoden der Raumzuweisung und -darstellung wiederholt und in den Kontext von GIS gestellt.
Raum und Zeit als Grundlagenkonzepte
Die Zeit
Wir beginnen mit der Zeit. Sie stellt in weiten Teilen der Welt ein einheitlich strukturiertes Zuordnungssystem dar. Konkret heißt das: Wir haben ein System von Zeitzonen und eine Konvention für die Datumsgrenze. Innerhalb der Zeitzonen wird die Zeit als lineares Kontinuum aufgefasst (vgl. Abb. 02-01). Selbst die Verwendung anderer Kalender, die eventuell abweichend benannt und gezählt werden, kann linear auf die uns vertrauten Weltzeitzonen umgerechnet werden. Das liegt in der physikalisch Auffassung begründet, das Zeit (mit Ausnahme archaischer/mythischer Zeitvorstellungen) ein lineares Bezugssystem darstellt. Auf einen Zeitpunkt folgt kontinuierlich der Nächste. Wir müssen schon Einstein’s Theorien bemühen um die Linearität der Zeit zu aufzulösen. Für die mit Hilfe von GI-Systemen möglichen Betrachtungsskalen ist Die Verwendung eines linearen Zeitverständnisses unproblematisch, jedoch, anders als die Abbildung des Raums, üblicherweise implizit bzw. optional implementiert.

Der Ort
Ohne eine exakte Verortung beliebiger Orte ist ein GIS ziemlich überflüssig, da wir dann nicht in der Lage sind räumlich zu messen, Eigenschaften räumlich zu vergleichen oder auch nur die Merkmale spezifischer Objekte geographisch darzustellen (Abb. 03-02). Für den sinnvollen Gebrauch von GI-Systemen ist die korrekte Verortung der Geoobjekte -oder anders ausgedrückt- die Georeferenzierung eine zentrale Technik. Es gibt eine Reihe von ähnlichen Ausdrücken für diesen Vorgang. Wir sprechen vom Georeferenzieren, Geolozieren, Verorten oder moderner vom Geotagging. Allen Begriffen ist gemeinsam, dass Merkmalsausprägungen an geographisch identifizierbare und kartographisch abbildbare Positionen gebunden werden.

Prinzipien der raumzeitlichen Kodierung
Namen und Adressen
Orte durch Benennung und Beschreibung identifizieren und lokalisieren zu können gehört zu den ältesten Kulturtechniken der Menschheit. Wir haben gelernt, dass geographische Informationen sich von anderen Informationstypen durch das Benennen eine räumlichen Komponente unterscheiden (Abb. 03-03).

Die Kombination von Namen und Ziffern, Deutschhaustrasse 10 in 35032 Marburg ist die postalische Kodierung für das Gebäude des Fachbereichs Geographie in Marburg. Auch wenn nicht alle Menschen eine auf diese Weise verschlüsselte Raumposition entschlüsseln können, gibt es ein weltweites Netz von Experten, die mit Hilfe dieser Kodierung einen Brief des Reisebüro Maluti Travel & Tours in Maseru, Lesotho zum Deutschen Haus in Marburg transportieren können. Umgekehrt gibt die Kodierung Maluti Travel & Tours, POB 14889, 0100 LNDL Building, Kingsway, Maseru Lesotho die Raumposition dieses Reisebüros an. Vielleicht kennen Sie aus Interesse oder Zufall die geographisch kodierte Position des Deutschhauses in Marburg, die Positionsangaben des LNDL Building in Maseru kennen Sie jedoch mit an Sicherheit grenzender Wahrscheinlichkeit nicht. Wiederum kennt auch der Postbote sicher nicht die geographischen Koordinaten der Empfängerorte, die er tagtäglich bedient – dennoch kommt die Post (meist) zuverlässig an ihrem Bestimmungsort an.
Das räumliche Referenzierungssystem hierfür funktioniert anders als über geographische Koordinaten, nämlich über Namen. Es ist eine Kette von Namenskodierung vom Nationalstaat über die Region bis hin zum Gebäude. Wenn sich dieser Name ändert, wie beispielsweise von Karl-Marx-Stadt in Chemnitz, bleibt selbstredend der geographische Raumbezug erhalten. Natürlich gibt es Ortsnamen, die vielfach vorkommen, so z.B. London oder Neunkirchen. Eine eindeutige Referenzierung nach dem vorgestellten System ist nur dann möglich, wenn der Ortsname eindeutig durch ein übergeordnetes Zuordnungssystem identifiziert werden konnte. Die wichtigste Schlussfolgerung ist, dass in GI-Systemen zur Vermeidung von Redundanzen, Fehlern und Unsicherheiten zur Referenzierung unbedingt ein möglichst allgemeingültiges, zweckdienliches System verwendet werden sollte (deshalb hat die Thurn und Taxis Post 1853 in Deutschland Ortsnamen mit einem Zahlenschlüssel kodiert, der eine abstrakte, nachvollziehbare Identifikation der Raumposition dieser Orte möglich macht).
Allen geographischen Informationen liegt eine eindeutige räumliche Zuordnung zugrunde.
Lineare Metrische Verortung
Ein System der systematischen Identifikation geographischer Orte haben wir mit den Postleitzahlen bereits kennen gelernt. Stellen wir uns nun folgenden Sachverhalt vor (Abb. 03-04):

Während der Zustellung des Briefes in Flensburg bleibt der Post-LKW auf der Bundesautobahn 7 liegen. Mit seinem mobilen Telefon steckt der Fahrer gerade im Funkloch und muss (natürlich nach Absicherung der Pannenstelle) zu Fuß zu einer Meldesäule. Auf seinem Weg läuft er an einem kleinen blauen Schild vorbei, auf dem 64,0 zu lesen ist. Angekommen an der Meldesäule gibt er seine Panne bekannt, gibt die Auskunft, dass sich das Pannenfahrzeug kurz hinter Kilometer 64,0 in Fahrtrichtung Nord hinter der Anschlussstelle Soltau befindet und die rechte Fahrspur blockiert. Wenig später hören Sie im Verkehrsfunk:
“1,5 km Stau zwischen der Anschlussstelle Soltau und der Anschlussstelle Bispingen wegen eines defekten LKW. Die rechte Fahrspur ist blockiert. Bitte fahren Sie vorsichtig”
Dieses alltägliche Beispiel verdeutlicht die Kombination aus Namen und metrischer eindimensionaler Positionsangabe als geographischem Verortungssystem. Da Sie die Autobahn unterwegs nicht verlassen können orientieren Sie sich von Ausfahrt zur Ausfahrt (Namen oder Ausfahrtskennziffer). Ihnen genügt daher die Information des Verkehrsfunks für eine ausreichend genaue Verortung des Staus.
Der Polizei oder dem Pannendienst genügt diese Angabe nicht. Sie hätten gerne z.B. zur Organisation der Bergung bzw. zur Einschätzung der Gefahren die exakte Kilometerangabe. Die Kilometrierung ist eine metrische Ortsangabe, die nur eine Dimension benötigt, da sie auf einer eindeutig definierten Strecke angeordnet ist. Ein solches Verortungskonzept ist metrisch also quantitativ. Es misst von einem definierten Ursprung/Start die Entfernung bis zum Zielpunkt/-ort. Diese sogenannte Lineare Referenzierung kann nur auf eindimensionale Geoobjekte Anwendung finden. Von diesen gibt es eine Vielzahl in unserem Alltag. Angefangen bei Autobahnen oder Gleisanlagen bis hin zu Rohr- und Versorgungsleitungen sind alle linearen, als Netzwerke ausgeprägten Strukturen linear referenzierbar.
Lineare Referenzen sind immer topologisch korrekt und können immer in geometrisch eindimensional messbaren Entfernungen angeben werden.
Versuchen Sie diesen Zusammenhang zu rekapitulieren und verschaffen Sie sich einen Überblick über die Pannensituation bzw. die Ortslage. Navigieren Sie mit Google Earth zum Schauplatz.
Betrachten Sie nun die nachfolgende Abbildung der Lininekarte der BAB 7. Sie zeigt exakt die gleichen Raum.

Navigieren Sie nun zur Linienkarte der BAB 7 und analysieren die Art der metrischen Verortung. Nutzen Sie die Legende, um die Fülle an räumlich verorteter Information nachzuvollziehen.
Katasterpläne - Geometrisch exakte maßstäbliche Raumabbildung
Im vorausgegangen Kapitel haben wir die eindimensionale metrische Referenzierung kennengelernt. Als zweidimensionale Erweiterung gibt es weltweit sogenannte Kataster. Es ist üblich, dass Kataster in Katasterplan und Katasterbuch unterschieden werden (Abb. 03-06). In Deutschland ist (wie in den meisten Ländern) die Führung und Pflege hoheitlich durch Vermessungsämter geregelt.

Dies liegt in der Notwendigkeit eines rechtskräftigen Nachweis von Eigentumsrechten (bekanntermaßen ein heikles Thema) begründet. Kataster bestehen seit der Antike für den persönlichen Nachweis von Steuerpflicht auf das Eignen von Liegenschaften. In den Kopfsteuerverzeichnissen wird an eine Person gebunden, die Steuerpflicht, bezogen auf Vermögen oder Liegenschaften, namentlich beschrieben.
Seit der Erfindung und Durchführung der exakten Vermessung der Welt durch Carl Friedrich Gauß (1777 – 1855) werden Kataster als flächendeckende Beschreibungen aller Flurstücke eines Landes durchgeführt. Für Deutschland wurde dies rechtlich durch den Code Civil Napoleons eingeführt und vom preußischen Staat vorbildlich umgesetzt. Der Kataster ist aufgeteilt in einen beschreibenden Teil – das sogenannte Liegenschaftsbuch – und in einen graphischen Kartenteil, die Liegenschaftskarte. In Beiden werden die geometrische Lage, die baulichen Anlagen, die Liegenschaften und die Art der Nutzung und Größe beschrieben sowie die Eigentumsverhältnisse und Rechtslasten festgelegt. Die Abbildung des Katasterplans stellt einen solchen graphischen Plan exemplarisch dar. Betrachtet man diese Abbildung genauer wird das Wort Plan verständlich. Die Parzellen sind zwar geometrisch exakt abgebildet, jedoch fehlt jegliches geographisches Referenzsystem. Vielmehr kann man eine Reihe von Ziffern für jede abgebildete Fläche identifizieren. Diese Ziffern verweisen auf die zugehörigen Eintragungen im Grundbuch. Analog zur linearen Referenzierung, die eindimensionale Geoobjekte metrisch referenziert, wird bei Katastern eine zweidimensionale metrische Referenzierung vorgenommen.
Katasterpläne sind immer topologisch korrekt und bieten immer geometrisch zweidimensional maßstäblich messbare Entfernungen und Flächen.
Verdeutlichen Sie sich erneut diesen Zusammenhang, indem Sie sich das Karten- bzw. Satellitenbild des heutigen Bukowsko in Google Maps anschauen. Vergleichen Sie dazu den Katasterplan von 1906.
Geographische Koordinaten - Breiten und Längengrade
Die vorangegangenen Beispiele zeigen wie mühsam und fehlerbehaftet die Orientierung an Objekten und ihren Namen ist. Sie zeigen auch, dass messbare, also geometrisch maßstäbliche Referenzierungssysteme nicht notwendig geographisch lokalisierbar sein müssen. Im Kapitel über Raumvorstellungen war die abstrakte Definition vom Raum und seinen Objekten bis zur Repräsentation der geographischen Informationen in spezifischen Datenobjekten Thema. Nun gilt es diese beiden Konzepte zu vereinen.
Ein leistungsstarkes System zur Referenzierung von geographischen Räumen sollte unbedingt folgende Grundeigenschaften zusammenführen:
- Skalenunabhängige Identifikation jedes Punktes auf der Erdoberfläche
- Messbarkeit, also mathematische Berechnungsvorschriften für alle geometrischen Operationen
- Zuordnung aller beliebig skalierten Attribute (z.B. Name, Temperatur, Qualität)
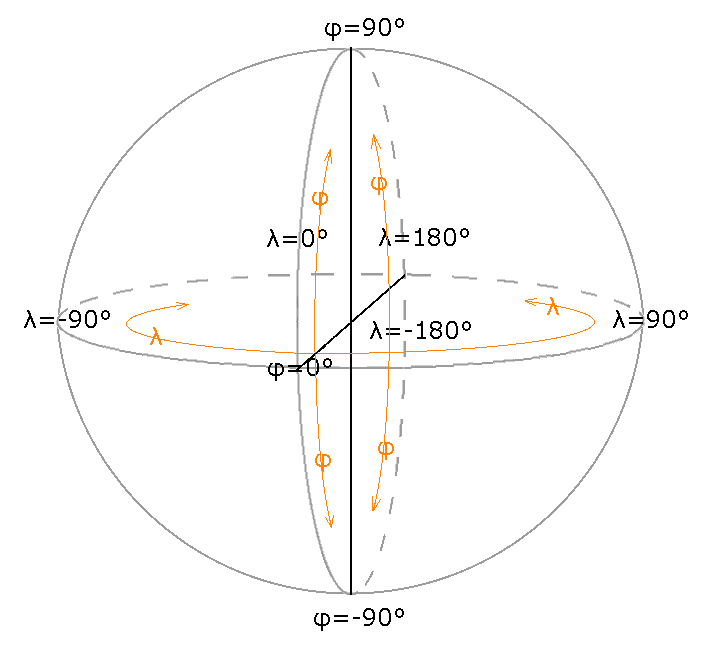
Die Erde gleicht in erster Annäherung einer Kugel. Daher liegt es nahe, die Punkte an der Oberfläche durch Kugelkoordinaten zu bestimmen. Da die Oberfläche einer Kugel bekannt ist genügen zur Bestimmung eines Punkts die zwei Winkel für den Azimuth (geographische Länge) Lambda und den Zenit (geographische Breite ) Phi (Abb. 03-07).

Überträgt man das Konzept der Kugelkoordinaten auf die Erde, so ergeben sich eine Reihe von Problemen. Das augenscheinlichste ist die Abplattung der Erde an den Polen, die durch die Erdrotation entsteht. Für die Bestimmung des Längengrads ist die Tatsache, dass die Erde ein Rotationsellipsoid mit großen und kleinen Halbachsen ist, unerheblich. Anders sieht dies für die Bestimmung der geographische Breite aus, da sich die Halbachsen der Erde um ca. 21,4 km unterscheiden (Abb. 03-08).
Die Abbildung zeigt das Rotationsellipsoid der Erde mit Kreisform der Breitenkreise (in der Äquatorebene Radius der großen Halbachse A) und der Längenkreise (kleine Halbachse an den Polen B). Das resultierende Maß für die Exzentrizität von ca. 1:298 gibt die Abplattung der Erde und damit die Streckenverschiebung bei der Bestimmung sphärischer Koordinaten an. Die zentrale Problematik der exakten Bestimmung der Erdoberfläche (im Sinne einer gleichförmigen Oberfläche zur Berechnung der sphärischen Koordinaten) liegt nun in der Entscheidung begründet, welche mathematische Repräsentation eines Ellipsoids als geeignetes Modell für das reale Rotationsellipsoid der Erde verwendet wird.
Da es sich immer nur um eine Annäherung an die ideale Erdform bezogen auf eine bestimmte Erdregion handelt, ist die Eignung des gewählten Ellipsoid als Referenz (Referenzellipsoid) von außerordentlicher Bedeutung zur Berechnung der Vermessungsnetze (Koordinatensysteme) und den daraus abgeleiteten Projektionssystemen (Abb. 03-09).
Ellipsoide und Bezugssysteme
In den vergangenen zwei Jahrhunderten wurden sehr unterschiedliche Referenzellipsoide entwickelt. Vor allem um regionale oder nationale Kartenwerke genauer ausführen zu können. Nun ist die Annäherung der Erdgestalt an die geometrische Figur eines Ellipsoids vergleichsweise einfach durchzuführen. Um eine möglichst genaue Position zu erhalten werden alle eingemessenen Punkte senkrecht auf das gewählte Referenzellipsoid projiziert. Bei einer kleinräumigen Betrachtungsweise ist die erreichbare Genauigkeit völlig ausreichend. Besuchen Sie die offizielle Online Datenbank für Referenzsysteme. Navigieren Sie zum EPSG Geodetic Parameter Set und suchen Sie nacheinander nach den Begriffen Bessel, Clarke, Krassowski und WGS84. Klicken Sie auf den View Link und vergleichen Sie die verfügbaren Parameter.
Das geodätische Datum
Bei einer kleinräumigen Betrachtungsweise ist die Genauigkeit einer auf ein Referenzellipsoid bezogenen Koordinatenbestimmung völlig ausreichend. Spannend ist, dass erst mit der Entwicklung von interkontinentalen Raketen in der ersten Hälfte des 20. Jhds. eine neue Dimension der Genauigkeit für die praktische Anwendung angestrebt wurde. In der Anwendung ist nämlich eine senkrechte Projektion auf das Ellipsoid unmöglich. Die senkrechte Projektion auf das auf Meeresniveau angenäherte Ellipsoid weicht um die sogenannte Lotabweichung von der wirklichen Senkrechten, wie sie durch ein gravitatives Schnurlot dargestellt wird, ab. Bei Vermessungen, die genauer sein sollen als etwa 0,5 Meter/1000 Meter (z.B. zur Berechnung der Ballistik von Interkontinentalraketen oder der Kontinentaldrift…), muss dieser Effekt berücksichtigt werden und die Messungen korrigieren zu können (Abb. 03-10).

Das Referenzmodell für die sich räumlich (und auch zeitlich) unterschiedlich ausprägende Schwere der Erde ist ein sogenanntes Geoid. Die Abbildung zum Erdschwerefeld visualisiert stark überhöht und farblich hervorgehoben diese Schwereanomalien.

Für genaue Messungen oder möglichst exakte Kartenprojektionen müssen beide Bezugskörper, das Ellipsoid und das Geoid, berücksichtigt werden. Die Abbildung zur Schwerevariation und zu einer weiteren Alternative zeigen die konzeptuellen Probleme bei der Berücksichtigung des Geoids und des Referenzellipsoids für eine exakte Berechnung von Koordinaten. In der klassischen Vermessungstechnik wird hierzu, möglichst im Zentrum des abzubildenden Erdausschnittes, ein Referenzpunkt gesetzt (Fundamentalpunkt), der zusammen mit dem Referenzellipsoid das sogenannte geodätische Datum ergibt.


Das geodätische System
Seit der Satellitenvermessung mit globalen Positionierungssystemen (GPS) sind viele, unabhängige Messungen bezogen auf die reale Erdgestalt verfügbar, so dass nicht länger vom geodätischen Datum gesprochen wird sondern vom geodätischen System
Das World Geodetic System 1984 (WGS 84) ist derzeit das am meisten verwendete geodätische Referenzsystem und dient als einheitliche Grundlage für Positionsangaben auf der Erde und im erdnahen Weltraum. Geodätische Systeme sind, anders als das geodätische Datum, global konstruiert und bestehen aus dem Referenzellipsoid, dem eingemessenen Geoid, und zwölf Fundamentalstationen, über die der Bezug zur Erdkruste über zeitabhängige Koordinaten bestimmt wird.
Betrachten Sie die Abbildung zu den Referenzellipsoiden. Sie zeigt schematisch (zweidimensional) die Verschiebungen von Referenzellipsoiden bezogen auf das Geoid, also die wahre Erdoberfläche. Die Sterne markieren den Mittelpunkt des jeweiligen Körpers. Versuchen Sie sich zu verdeutlichen welche Parameter notwendig sind um diese Verschiebung durchzuführen.

Kartenprojektionen in GI-Systemen
Die geographischen Winkel Länge und Breite referenzieren jeden Punkt auf der Oberfläche der Erde mit hoher skalierbarer Genauigkeit. Sie beziehen sich auf die wohldefinierte, dreidimensionale idealisierte Oberfläche der Erde. Diese Körpergestalt der Erde nutzt bekannte und durch Konvention festgelegte Referenzpunkte: das Königliche Observatorium von Greenwich für den Bezugsmeridian, das Schwerkraftzentrum der Erde und die Halbachsen des Referenzellipsoids der Erde als Annäherung an ihre wahre Gestalt.
Mit Hilfe dieser Parameter sind ausreichend genaue Lokalisationen aller Geoobjekte möglich. Gleiches gilt für die Analyse und Berechnung ihrer geometrischen Beziehungen. Historisch gesehen sind diese Aufgaben nicht auf einem Sphäroid durchgeführt worden sondern auf zweidimensionalen Karten die als projiziertes Abbild der Erde verwendet wurden. Auch heute besteht für sehr viele Anwendungen und Daten die Notwendigkeit eine verebnete zweidimensionale Projektionen der Erdoberfläche zu nutzen. So sind:
- alle Ein- und Ausgabekarten zweidimensional
- alle Rasterdatensätze (Satellitendaten, Luftbilder) zweidimensional, da quadratische Netze sich nicht verzerrungsfrei und ohne Überschneidungen oder Lücken auf eine Kugel aufbringen lassen
Eine Kartenprojektion ist nun eine mathematische Methode mit der man die gekrümmte Oberfläche der dreidimensionalen Erde auf die flache, zweidimensionale Karte überträgt. Dies erfolgt in zwei Schritten:
- Auswahl eines geeigneten Referenzmodells für die Kugelgestalt der Erde
- Transformation der geographischen Koordinaten (Länge und Breite) in ein kartesisches Koordinatensystem (x und y oder Rechtswert und Hochwert)
Im euklidischen Raum wird durch Bestimmung der x,y Koordinate ein Punkt in der Ebene (=zweidimensional) verortet. Obwohl der dreidimensionale euklidische Raum auch die aus geographischem Winkel bestimmten Positionen abbilden kann, ist aus den oben genannten Gründen die Projektion von sphärischen Koordinaten in ein zweidimensionales kartesisches Bezugssystem üblich und meistens sinnvoll.
Kartenprojektionen können also als Transformation der von sphärischen Koordinaten der geographische Länge und Breite in kartesische Koordinaten y,x (Hochwert, Rechtswert) verstanden werden.
Da es sich bei allen Transformationen um sphärische Trigonometrie handelt und Geo-Datensätze beliebig unterschiedliche Referenzellipsoide und/oder geodätische Systeme als Grundlage haben (können), ist es von essentieller Bedeutung für das Arbeiten mit GI-Systemen diese Parameter und ihre Merkmale zu kennen und interpretieren zu können.
Kartenprojektionen werden üblicherweise nach der Projektionsfläche, oder der Lage der Abbildungsfläche oder den Abbildungseigenschaften eingeordnet. Da es in GI-Systemen vor allem auf Genauigkeit und Qualität ankommt ist eine Klassifizierung nach den Abbildungseigenschaften von hervorgehobener Bedeutung. Projektionen müssen die abgebildeten Flächen der Erdoberfläche verzerren. Es gibt keine 1:1-Projektion von Orten und Flächen aus einem dreidimensionalen Bezugssystems auf eine zweidimensionale Karte:
- Längentreue Projektion (engl.: equidistance, equal distance): Maßstäblich genaue Entfernungen auf der Karte
- Flächentreue Projektion (engl.: equal area): Maßstäblich genau Flächeninhalte auf der Karte
- Winkeltreue Projektion (engl.: conformity): Exakte Winkelabbildungen auf der Karte
- Vermittelnde Projektion: Kompromisse zwischen Längentreue, Flächentreue oder Winkeltreue
Die resultierenden Qualitätsminderungen müssen gemäß der Zielsetzung und Fragestellung die Kriterien für die Auswahl eines geeigneten Projektionsverfahrens vorgeben. Da alle drei Kriterien unerfüllbar sind (außer auf einem maßstabsgetreu verkleinerten exakten dreidimensionalen Erdabbild) sind die unterschiedlichsten Projektionsverfahren und Bezugskörper zur Minimierung dieser Fehler entworfen worden.
Die Wahl der Projektion ist abhängig von der Zielsetzung hinsichtlich der Darstellung der Daten. Werden mit den Daten räumliche Analysen durchgeführt, muss eine adäquate geodätische Projektion gewählt werden.
Denken Sie mit…
Besuchen Sie die folgende Webseite die ihnen interaktiv Kartenprojektionen visualisieren hilft und machen Sie sich interaktiv ein Bild von den Eigenschaften und Auswirkungen der unterschiedlichen Kartenprojektionen. Betrachten Sie zumindest folgende Netzentwürfe:
- Lambert’sche konforme Schnittkegelprojektion
- Lambert’sche Azimutalprojektion
- Normale und transversale Mercatorprojektion
- Mollweideprojektion
- Robinson Projektion
