Topologische Abfragen

Während geometrische Selektionskriterien Geoobjekte anhand ihrer Position und thematische Abfragen Elemente bezüglich ihrer Eigenschaften identifizieren, basieren die topologischen Suchkriterien auf der relativen Anordnung der Geoobjekte im Raum. Ein typisches Merkmal relativer Verortung ist der Vergleich mit anderen Geoobjekten z. B. wie „nächster“, „Teil von“ oder „innerhalb“. Die räumlichen Lagebeziehungen werden in GI-Systemen als Topologie bezeichnet. Topologische Beziehungen werden aus den geometrischen Primitiven aufgebaut: Punkte (einfachstes Element), Linien (Reihe von verbundenen Punkten), Flächen (Reihe von verbundenen Linien). Anhand dieser geordneten Struktur ist das GI-System in der Lage, die topologischen Beziehungen zu erkennen und entsprechende Analysen durchzuführen.

Folglich beschäftigt sich die Topologie mit den räumlichen und strukturellen Eigenschaften der geometrischen Objekte unabhängig von ihrer Ausdehnung und ihrer geometrischen Form. Zu den topologischen Eigenschaften gehören die Anzahl der Dimensionen eines Objektes und die möglichen Beziehungen zwischen den Dimensionen. Die Topologie ermöglicht Analysefunktionen wie die Verfolgung einer Strömung entlang verbundenen Linien eines Netzwerkes, das Vereinigen benachbarter Flächen mit ähnlichen Eigenschaften etc.

Es ist allerdings essentiell zwischen den zwei üblichen Datenformaten zu unterscheiden: Topologische Operationen auf Vektordaten sind völlig unterschiedlich zu topologischen Operationen auf Rasterdaten. Daher sind die Algorithmen, die für Vektordaten gültig sind, nicht ohne weiteres auf Rasterdaten anwendbar. In der Folge beschränken wir uns auf die topologischen Operationen bei Vektordaten.

Typisierung topologischer Beziehungen

Eine einfache Methode zur Typisierung topologischer Beziehungen wurde von (Egenhofer et al. 1993 vorgeschlagen. Sie wird als 9-Intersection Schema bezeichnet. Das Intersection-Schema ist ein elegantes Konzept zur Klassifikation von topologischen Konfigurationen. Die grundsätzliche Idee basiert auf dem Konzept, dass jedes Element aus einem Rand (b), einem Inneren (i) und einem Komplement (e) besteht. Die Konzepte von Innerem, Rand und Komplement (Äußerem) sind in der allgemeinen Topologie definiert.

Abbildung 03-16: Topologische Beziehungennach Egenhofer (GITTA 2005)

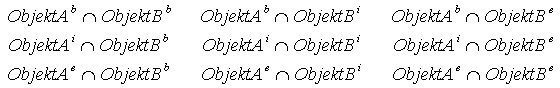
Wenn die der äußeren Umgebung (Komplement) entsprechende Zeile und Spalte aus der Matrix weglassen wird, erhält man das 4-Intersection-Schema, welches häufig als vereinfachte Grundlage für die Untersuchung topologischer Beziehungen verwendet wird, aber nicht so mächtig wie das 9-Intersection-Schema ist.

Abbildung 03-17: Topologische Beziehungen nach Egenhofer (GITTA 2005)

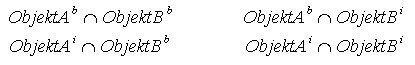
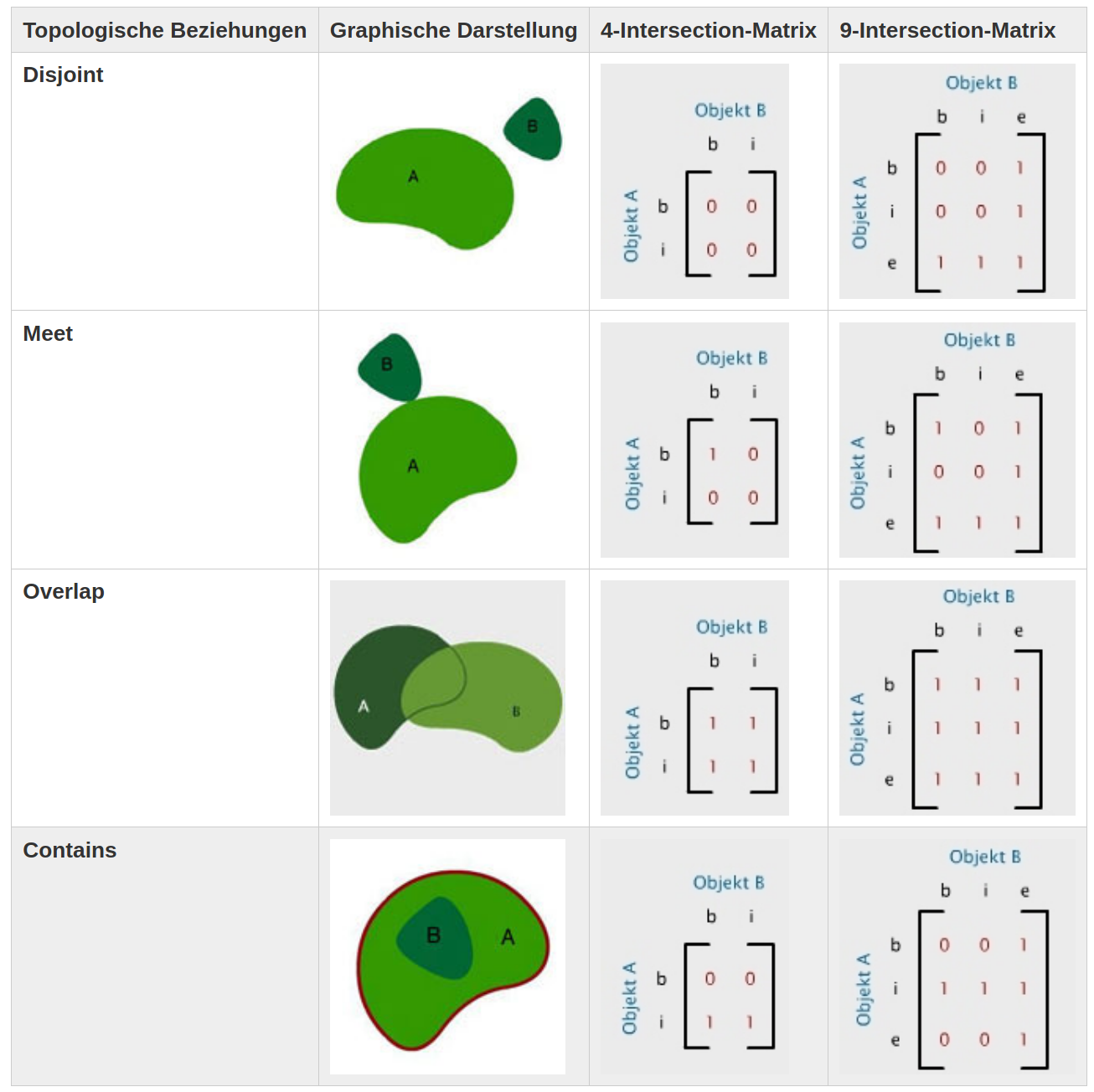
Topologische Beziehungen kompakt

Versuchen Sie anhand der folgenden Tabelle das 9-I-Schema und das 4-I-Schema (Egenhofer et al. 1993 für einige typische topologische Beziehungen zwischen zwei Flächen nachzuvollziehen. Die Beziehungen sind durch die Werte 0 oder 1 gegeben. Jedes Paar hat eine leere (0) oder eine belegte (1) Schnittmenge.

Abbildung 03-18: Topologische Beziehungen nach Egenhofer (GITTA 2005)

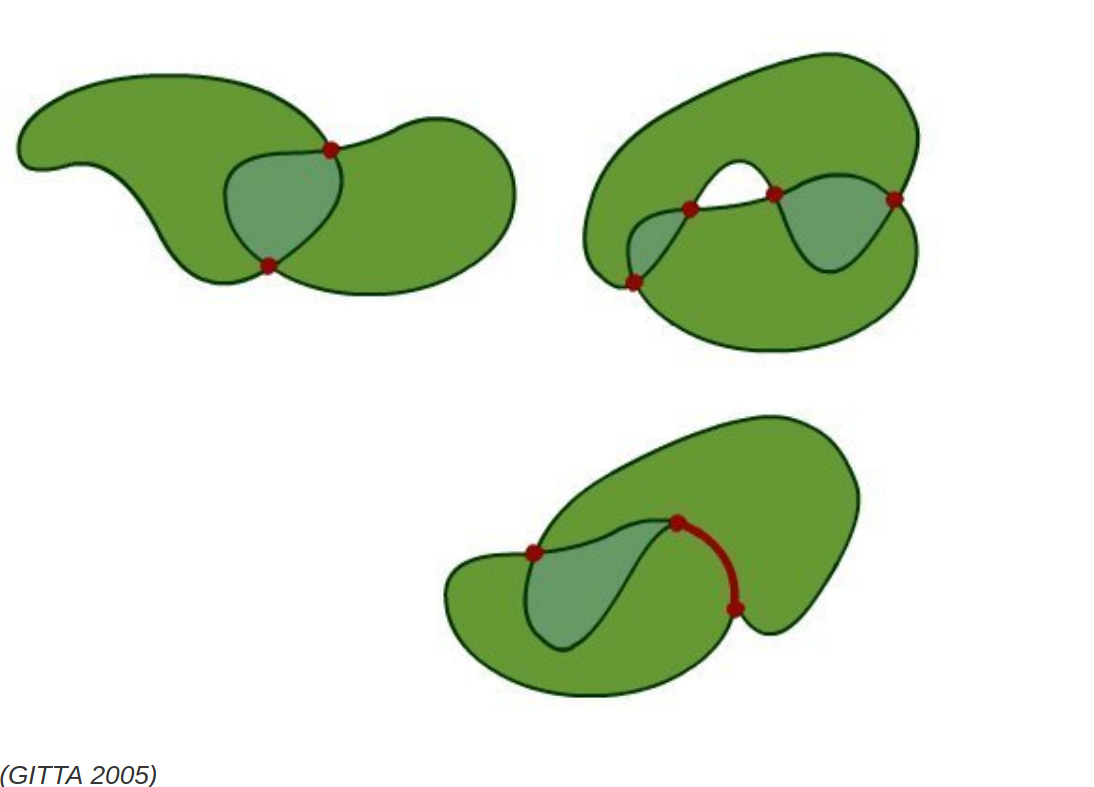
Denken Sie nach…

• Betrachten Sie die nachfolgende Abbildung und versuchen Sie die korrekte 4- bzw. 9-Intersection-Matrix zuzuordnen. Können Sie ein Problem artikulieren?

Abbildung 03-19: Topologieübung (GITTA 2005)

Topologische Operatoren

Die topologischen Operatoren sind Bestandteile der räumlichen Analysefunktionen eines GIS und dementsprechend grundlegend. Diese sind in den kommerziellen GIS wie ArcView, ArcInfo, Geomedia, MapInfo u. a. aber auch in den Open-Source-Paketen wie QGIS implementiert. Jedes System verfügt über eine eigene Formulierung der topologischen Abfragen; einige davon erlauben es, die topologischen Abfragen mittels SQL auszuführen. Geographische Datenbanken („spatial databases“) wie z.B. Oracle oder PostGis werden laufend weiterentwickelt und stellen solche Werkzeuge für die Datenverwaltung und ihre Funktionalitäten den GIS zur Verfügung. Sie implementieren weitere topologische Operatoren aus dem GIS-Bereich, welche effizient auf die entsprechende Datenstruktur anwendbar sind. Die folgende Tabelle listet einige Funktionen sowie den entsprechenden Operator, der von Geomedia, Oracle Spatial, ArcGIS und QGIS angeboten wird, auf.

TOPOLOGISCHE BEZIEHUNG	ORACLE	GEOMEDIA	ArcGis	QGIS
Disjoint	disjoint	-	are within a distance of	außerhalb
Meet	touch	meet	-	berührt
Overlap	overlap by intersect	overlap	intersect	überlappt
Contains	contains	entirely contains	completely contains	enthält
Inside	covers	are entirely contained by	contains the center of	innerhalb
Covers	inside	contain	have their center in	innerhalb
Coverered by	coveredby	are contained by	are completely within	innerhalb
Equal	equal	are spatially equal	-	gleich

Tabelle 03-04: Topologische Operatoren (GITTA 2005)

Topologische Beziehungen

Die wichtigsten topologischen Beziehungen zwischen Geoobjekten, die im GIS-Bereich genutzt werden, sind in der Folge aufgelistet. Dabei ist zu beachten, dass grundsätzlich alle drei Geometrietypen (Punkt, Linie und Fläche) des Vektordatenmodells berücksichtigt werden.

• Disjunkt (Disjoint) Objekt A und Objekt B weisen keine Schnittfläche auf. Test auf Getrenntheit (Disjoint) der Ausgangsgeometrie und einer anderen Geometrie.

• Meet Objekt A und Objekt B berühren sich an den Grenzlinien. Test auf Berührung (Touch) der Ausgangsgeometrie und einer anderen Geometrie. Die Ränder schneiden sich, nicht aber das Innere der beiden Geometrien. Zwei Geometrien berühren sich, wenn sich nur die Ränder schneiden.

• Overlap Objekt A und Objekt B überschneiden sich. Test auf Überschneidung (Intersect) der Ausgangsgeometrie und einer anderen Geometrie (Umkehrung von Disjunkt). Überlappung mit Getrenntheit: Das Innere eines Objekts schneidet den Rand und das Innere des anderen Objekts, die beiden Ränder schneiden sich aber nicht. Das ist der Fall, z. B. wenn eine Linie außerhalb eines Polygons (Fläche) beginnt und im Inneren des Polygons endet. Überlappung mit Überschneidung: Die Ränder sowie das Innere der beiden Objekte schneiden sich. Wenn eine Geometrie eine andere schneiden soll, so muss die Geometrie des Schnittes einer kleineren Dimension in der größeren vorhanden sein
  • Punkte können keine Punkte, Linien oder Flächen schneiden.
  • Linien
    • Können keine Punkte schneiden
    • Können weitere Linien schneiden » Schnitt = Punkte.
    • Können Polygonen schneiden » Schnitt = Linien (Punkte).
• Contains Objekt A enthält Objekt B. Test, ob die Ausgangsgeometrie eine andere Geometrie umschließt (Contains). Das Innere und der Rand eines Objekts sind vollständig im Inneren eines anderen Objekts enthalten. Eine Geometrie kann kein Geometrie höherer Ordnung (Dimension) enthalten; d. h.:
  • Punkte können keine Linien oder Fläche enthalten.
  • Linien können keine Fläche enthalten.

• Inside Objekt B liegt innerhalb Objekt A. Das Gegenteil zu „enthalten“. Wenn A innerhalb B liegt, so enthält B A.

• Covers Objekt A deckt Objekt B. Das Innere eines Objekts liegt vollständig im Inneren des anderen Objekts, und die Ränder schneiden sich. Eine Geometrie kann keine Geometrie höherer Ordnung (Dimension) enthalten; d. h.:
  • Punkte können keine Linien oder Flächen enthalten.
  • Linien können keine Fläche enthalten.

• Covered by Objekt B ist von Objekt A bedeckt. Das Gegenteil zu „decken“. Wenn A von B gedeckt ist, so deckt B A.

• Equal Objekt B und Objekt A stimmen überein. Test auf Gleichheit (Equals) der Ausgangsgeometrie und einer anderen Geometrie. Das Innere und der Rand eines Objekts liegen auf dem Rand des zweiten Objekts (und das zweite bedeckt das erste Objekt). Diese Beziehung besteht z. B., wenn eine Linie genau auf den Rand einer Fläche fällt. Die Koordinaten aller einzelnen Bestandpunkte müssen gleich sein. Die verglichenen Geometrien müssen ebenfalls gleich sein; d. h.:
  • Punkte = Punkte
  • Linien = Linien
  • Polygone = Polygone

Sie können die topologischen Beziehungen anhand der folgenden Tabelle nachvollziehen. Die Auflistung zeigt die am häufigsten vorkommenden topologischen Beziehungen:

Abbildung 03-19: Topologische Beziehungen von unterschiedlich dimensionalen Vektordaten (GITTA 2005)

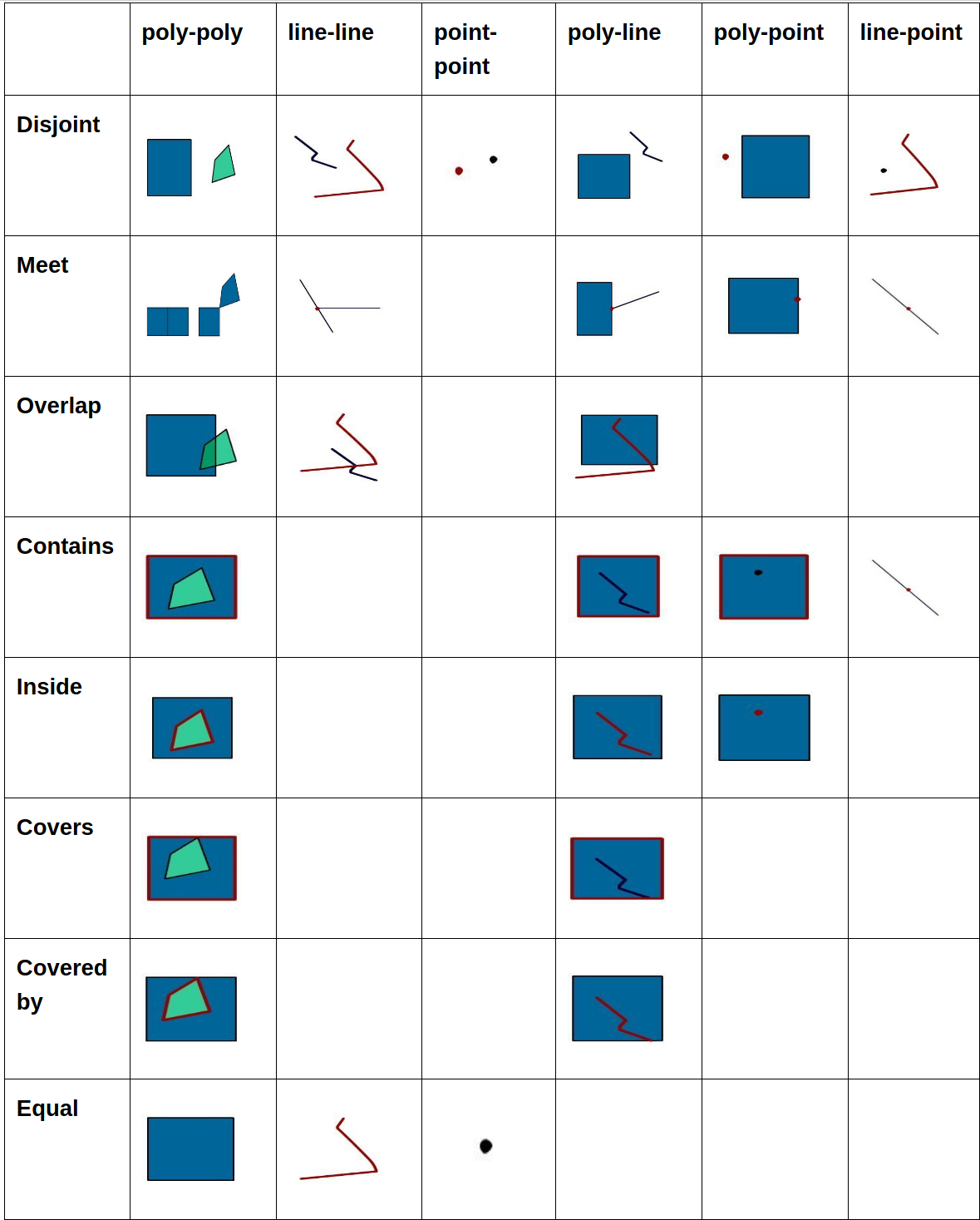
Häufige topologische Beziehungen

Die Beziehungen zwischen Flächenobjekten und anderen Objekten kommen am häufigsten vor. Nachfolgend einige mögliche topologische Abfragen in diesem Zusammenhang.

Abbildung 03-19: Topologische Abfragen von unterschiedlich dimensionalen Vektordaten (GITTA 2005)

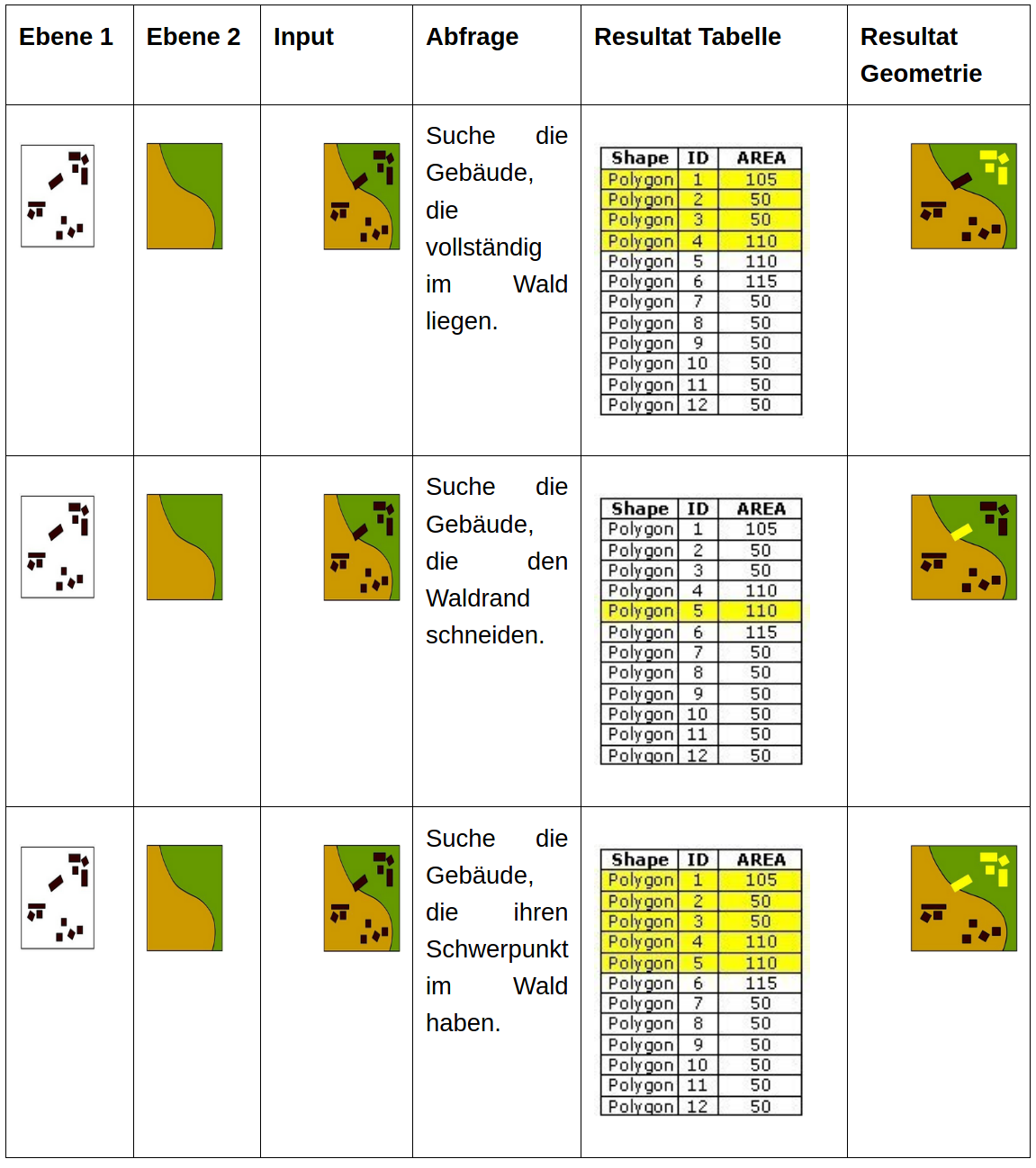
Denken Sie nach…

• Versuchen Sie zu identifizieren, welche der topologischen Operatoren Elemente der logischen und vergleichenden/arithmetischen Operatoren beinhalten