Geometrische Abfragen
Geometrische Abfragen messen die Fläche oder den Umfang eines Objektes bzw. die Distanz oder Richtung =zwischen zwei Objekten. Bei der Erörterung geometrischer Abfragen müssen die Raster- und Vektordatenmodelle aufgrund ihres völlig unterschiedlichen Raumkonzepts getrennt betrachtet werden. Im Sinne einer Relation ist die Geometrie eine weitere Eigenschaft eines Geoobjektes.
Die wichtigsten geometrischen Abfragen (Messfunktionen) sind in der Folge beschrieben:
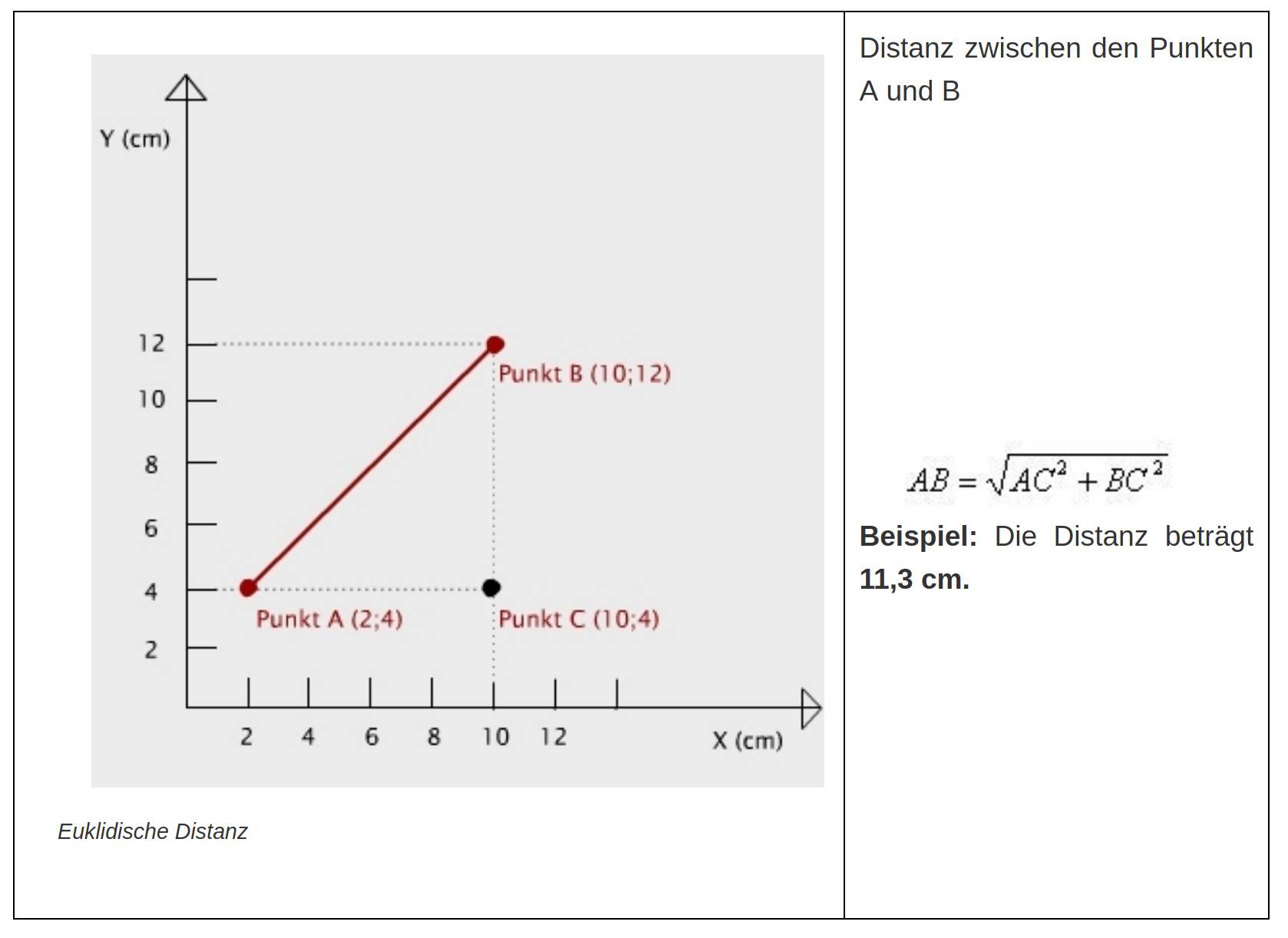
Euklidische Distanz im Vektormodell
Für Vektordaten wird die Distanz zwischen zwei Objekten einfach nach dem Theorem von Pythagoras berechnet und entspricht dem kürzesten Abstand.
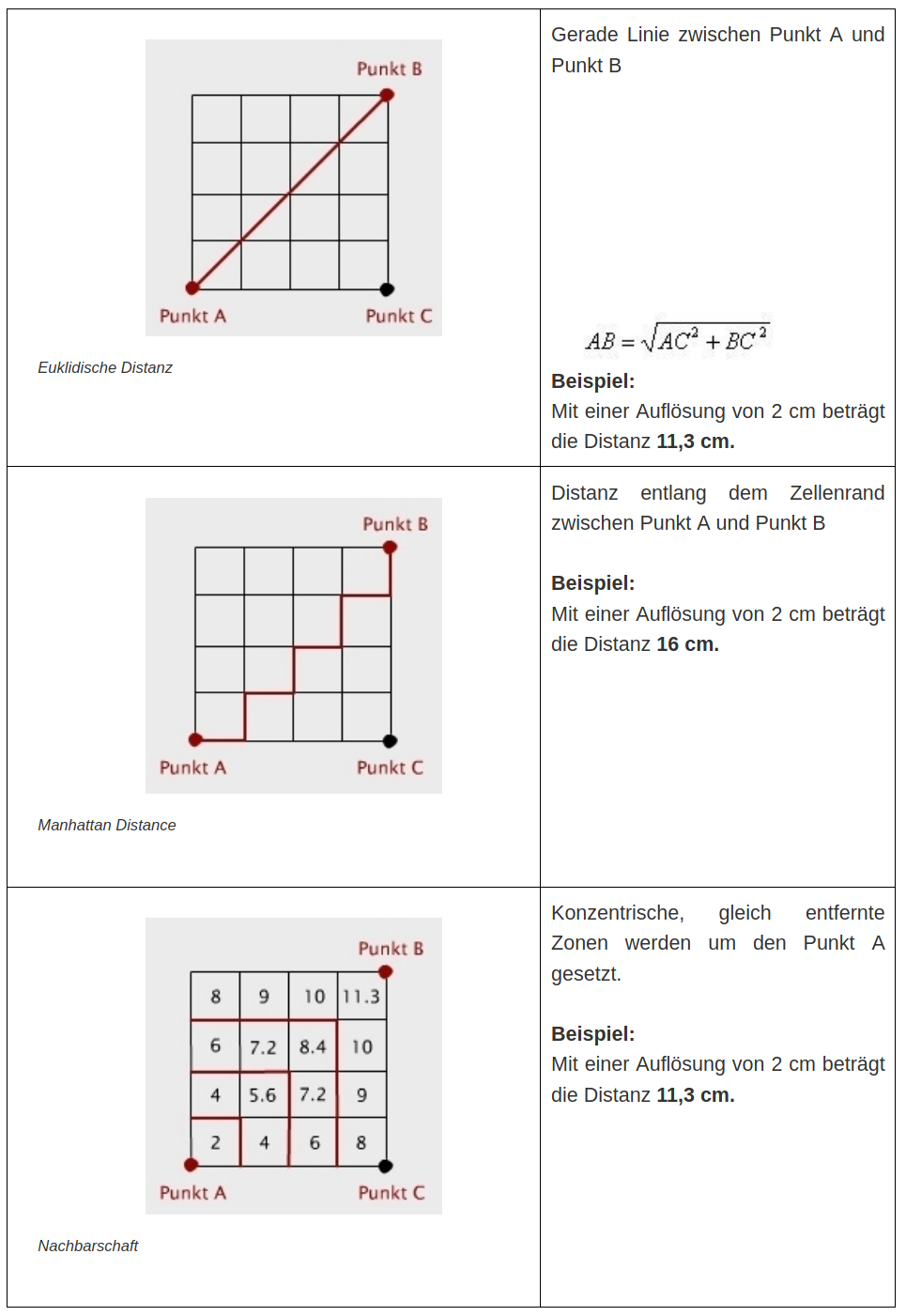
Euklidische Distanz Rastermodell
Im Rastermodell können drei verschiedene Ansätze zur Messung von Distanzen zwischen Punkten angewandt werden.
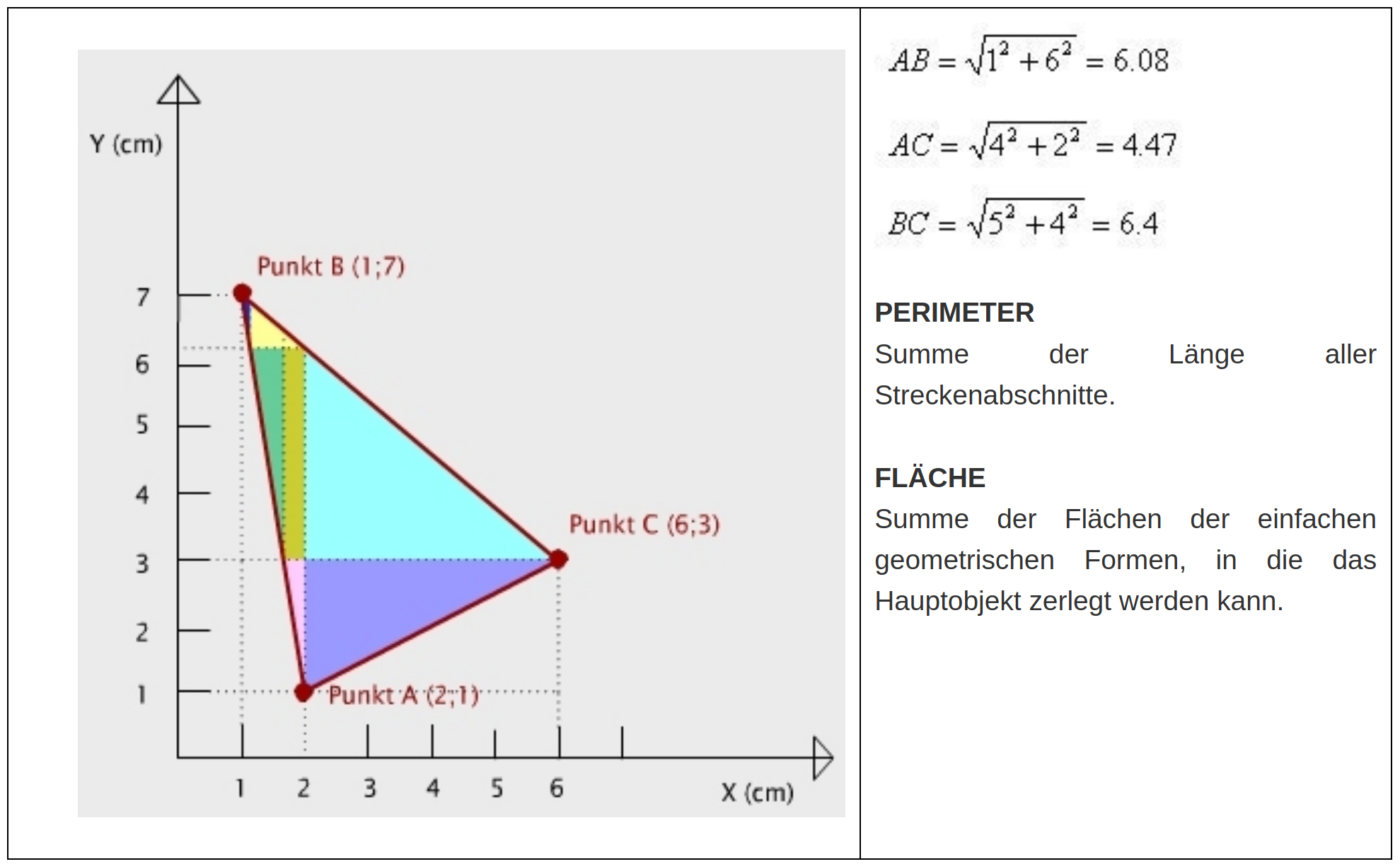
Ausdehnung Vektormodell
Rastermodell
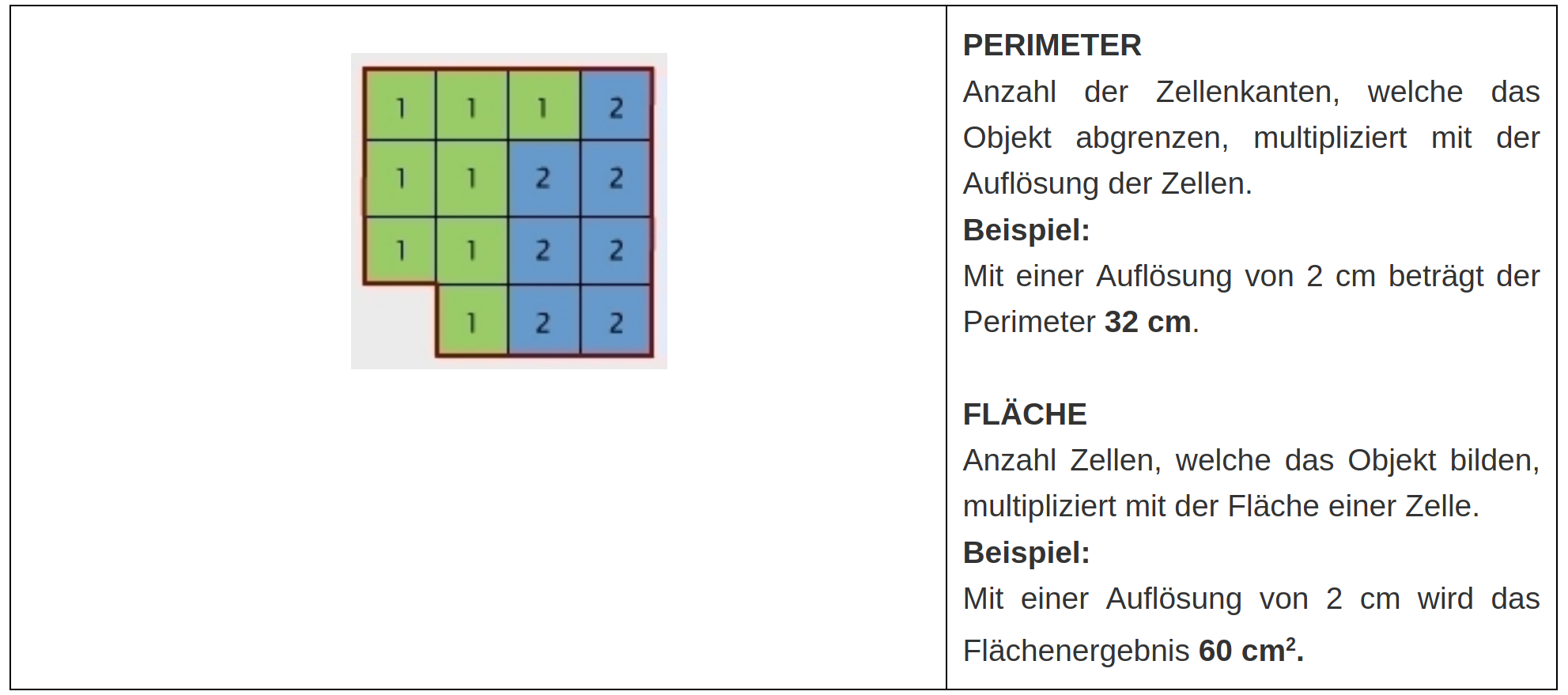
Distanzzonen: Distanzpuffer und Distanztransformation
Neben der Ermittlung von (kürzesten) Distanzen zwischen Objekten ist eine weitere wichtige Anwendung in einem GIS das Ermitteln von Distanzzonen. Mit dieser Funktion wird jeder Raumstelle ein Distanzwert zum entsprechend nächsten Bezugsobjekt zugewiesen. Die Bildung von Distanzzonen ist für Vektor- und Rastermodell in der Lösung sowie in der Verwendung deutlich verschieden.
Vektormodell
Vektormodelle werden meist zur Modellierung von randscharfen Phänomenen verwendet. Distanzzonen im Vektormodell ergeben wiederum klare, randscharfe Polygone. Es wird deshalb der Begriff Distanzpuffer (engl. buffer) anstelle des allgemeineren Begriffs Distanzzone verwendet. Die Berechnung eines solchen Distanzpuffers ergibt als Resultat immer eine Fläche (d. h. ein Polygon), egal ob von Punkten, Linien oder Flächen ausgegangen wird. Gesucht ist die Umrißlinie (Grenzlinie) dieser resultierenden Fläche, die in einem definierten Abstand das Ausgangsobjekt umrandet (vgl. untenstehende Animation). Der Berechnung von Distanzpuffern liegt eine euklidische Metrik zugrunde. Weitergehende Möglichkeiten, wie sie im Rastermodell einfach realisiert werden können, sind nur aufwendig erreichbar. So können ineinander geschachtelte Distanzzonen (z. B. 0–500 m, 501–1000 m, 1001–2000 m) nur durch wiederholte Berechnung und anschliessendes Verschneiden der Puffer als Polygone (engl. polygon overlay) realisiert werden. Die Möglichkeiten der Pufferbildung im Vektormodell sind beschränkter als beim Rastermodell. Dennoch gibt es einige Möglichkeiten, Distanzpuffer zu variieren (Animation unten):
- Die Form eines Puffers kann variiert werden. So kann z. B. das Ende von Puffern um Linien entweder flach oder rund sein.
- Pufferdistanzen können abhängig von einem Attributwert der Ausgangsobjekte berechnet werden. Beispielsweise bestimmt die Sendeleistung von Mobilfunkantennen ihre Reichweite.
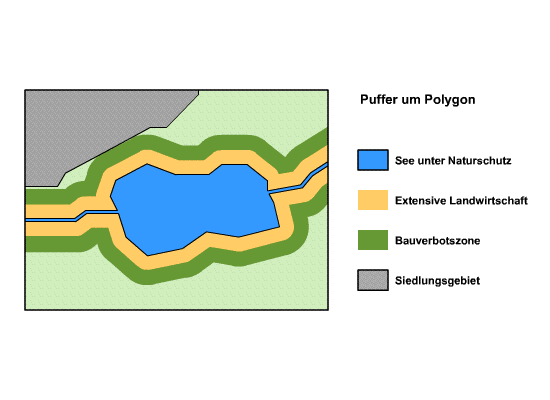
- Puffer können auch nur einseitig gebildet werden, z. B. Bauverbotszone um einen See.
Rastermodell
Die Bildung von Distanzzonen im Rastermodell weist jeder einzelnen Rasterzelle einen Distanzwert entsprechend ihrer Distanz zur nächstgelegenen „Quellenzelle“ zu. Dadurch ergibt sich ein quasi-kontinuierliches Resultat. Da der Raum also entsprechend der Distanz zu bestimmten Objekten transformiert wird, kann im Rastermodell von einer Distanztransformation gesprochen werden: Im Rastermodell kann für die Distanztransformation eine geeignete Metrik gewählt werden: euklidische Metrik, Manhattan-Metrik oder eine Metrik, die zusätzlich zur Manhattan-Metrik (4er-Nachbarschaft der Rasterzellen) auch die diagonalen Nachbarn (8er-Nachbarschaft) einbezieht. Zusätzlich können auch Wegkosten oder Wegzeiten als Kostenoberflächen berücksichtigt werden. Kostenoberflächen enthalten Informationen über den pro Zelle variierenden Aufwand, der geleistet werden muss, um eine Distanz zurückzulegen. Eine quasi-kontinuierliche Raster-Distanztransformation kann man elegant durch eine einfache Einordnung in klassierte Distanzzonen umformen (z. B. Distanzzonen bis 250m, bis 500m usw.). Die Genauigkeit des Resultats richtet sich allerdings direkt nach der Auflösung (Maschenweite) des Rasters.
| Vektormodell | Rastermodell | |
| Bezeichnung | Distanzpuffer | Distanztransformation |
| Metrik | euklidische Metrik liegt der Berechnung zugrunde | verschiedene Metriken sind möglich |
| Modellierung | randscharfe und klar definierbare Phänomene | Phänomene, die eher kontinuierlich über den Raum variieren |
| Distanzzonen | Verschneidung der Distanzpuffer mit polygon overlay. Zusätzliche Variationen: Einseitige Puffer / Gewichtete Puffer(abhängig vom Attributwert des Ausgangsobjekts) / Form (flache/runde Enden) bei Linien | Klassierung der Distanztransformation (reclassify) |
| variable Kosten | unmöglich | Einbezug von Kostenoberfläche als Aufwand der Distanzüberwindung möglich |
| Genauigkeit | abhängig von der Datengenauigkeit und Rechenpräzision | von der Auflösung des Rasters abhängig. |
Erstellen eines Distanzpuffers im Vektormodell
Distanzpuffer um Punkte sind Kreisflächen. Die Punkte in der folgenden Abbildung repräsentieren Standorte von Mobilfunkantennen mit unterschiedlicher Sendeleistung. Dabei ist die äusserste Linie die maximale Reichweite bei gegebener Sendeleistung. Die Distanzpuffer sind hier mit Attributwerten der Ausgangsobjekte gewichtet. Auf der Karte wird ersichtlich, welche Teile der Siedlungsfläche mit einem Empfang abgedeckt sind und welche nicht.
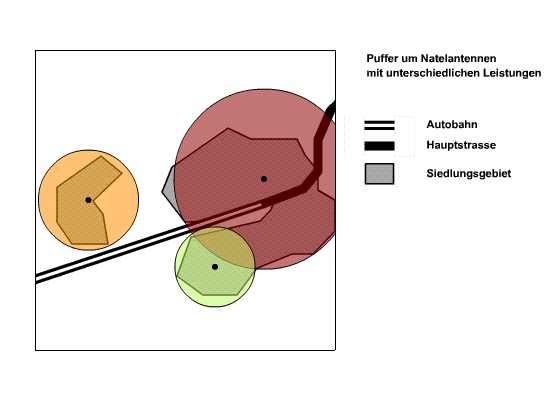
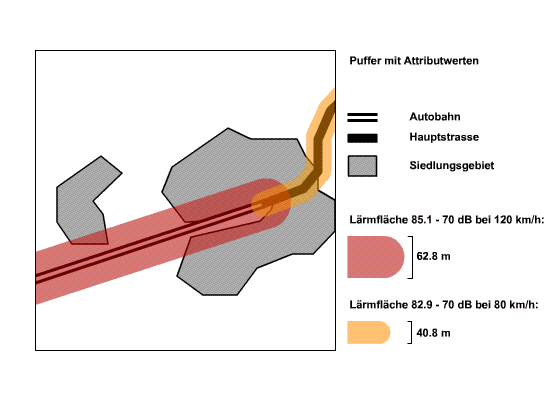
Das nächste Beispiel beschäftigt sich mit Distanzpuffern entlang von Linien. Die Linien sind in diesem Fall Strassen unterschiedlicher Kategorien. Durch die Einteilung der Strassen ist die Höchstgeschwindigkeit bekannt: Autobahnen 120 km/h und Hauptstrassen 80 km/h. Über ein Immissions-/Emissionsmodell für Strassenlärm (vgl. Lärmorama wurden die Distanzpuffer für einen Grenzwert von 70 dB abhängig von der erlaubten Höchstgeschwindigkeit berechnet. In das Modell fließen hauptsächlich drei Parameter ein: durchschnittliche Geschwindigkeit, durchschnittliche Anzahl Fahrzeuge pro Stunde und der Lastwagenanteil. Hindernisse usw. wurden keine berücksichtigt. Es wird davon ausgegangen, dass der Schall sich ungehindert im Raum ausbreiten kann. Die so entstandenen Flächen decken ein Gebiet von 85,1 dB an der Verkehrsachse und bis 70 dB an der Umrisslinie des Distanzpuffers (beziehungsweise von 82,9 dB bis 70 dB) ab. Dies bedeutet, dass Pufferfläche bezüglich der Beschallung (Immissionswert) nicht homogen ist. Häufig interessiert die Grenzlinie bzw. ein Grenzwert, der mit der Umrisslinie der Pufferfläche markiert ist. Interessant ist diese Fläche aber, wenn z. B. herausgefunden werden möchte, wie groß die Fläche (bzw. Anzahl Einwohner) des Siedlungsgebiets ist, die einem Lärm von 85,1 dB bis 70 dB ausgesetzt ist. Möchte man eine Abstufung bzw. Verschachtelung der Immissionswerte darstellen, müssen mehrere Distanzpuffer mit den jeweiligen Immissionswerten berechnet werden.
Das letzte Beispiel zeigt einseitige Distanzpuffer, die aufgrund eines Gesetzes festlegt wurden, das bestimmt, welche Abstände um ein Naturschutzgebiet für extensive Landwirtschaft (schonender Umgang mit der Natur) und einem allgemeinem Bauverbot gelten.