Raum im GIS
Bisher haben wir ständig und ohne besondere Vorüberlegungen mit den Begriffen Raum und Zeit gearbeitet. Um die bereits im Abschnitt Objekte im Raum vorgestellten Raumkonzepte (diskrete Geoobjekte, kontinuierliche Räume) in GI-Systemen und letztlich auch allgemein wissenschaftlich nutzbar zu machen, müssen wir diese Begriffe konkreter fassen.
Der Raum in GI-Systemen wird in Anlehnung an die Mathematik und Physik als dreidimensionaler euklidischer Raum verstanden. Aus dem Mathematikunterricht kennen wir die euklidische Ebene (mit 2 Dimensionen) und den euklidischen Raum (mit 3 Dimensionen). Am einfachsten lässt sich der euklidische Raum mit Hilfe eines kartesischen Koordinatensystems beschreiben, in dem die Koordinaten entlang senkrecht zueinander stehender Achsen aufgetragen werden (vgl. Abb. 02-1).
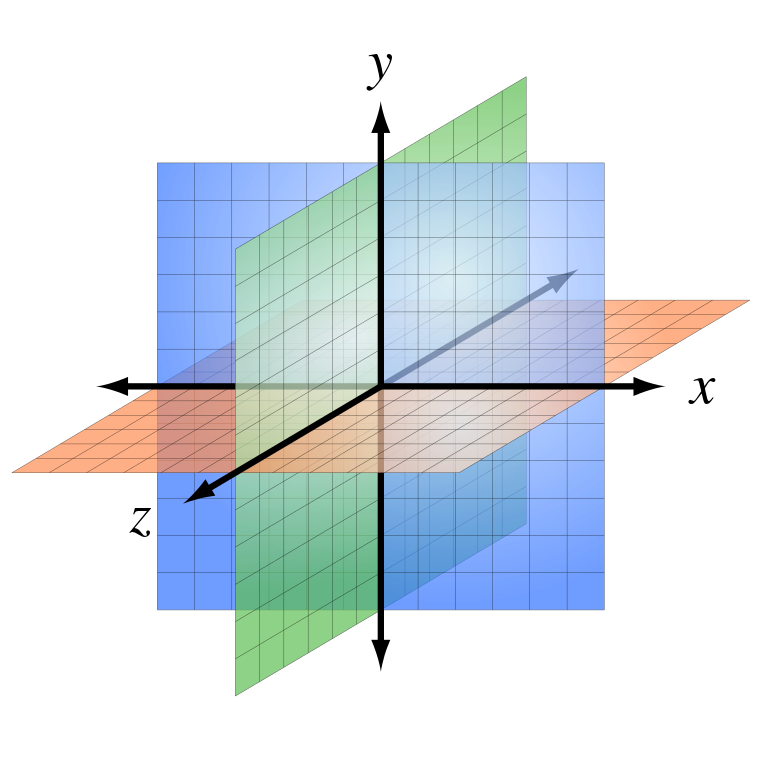
Die Raumrichtungen
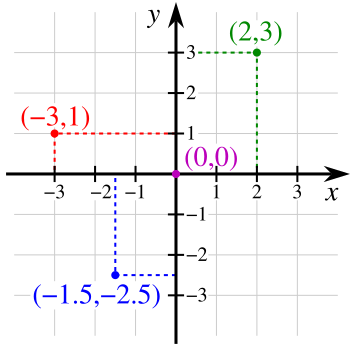
Bisher haben wir von Geoobjekten als definierte Objekte mit eindeutiger Lage (Koordinaten) gesprochen. Mit Hilfe der Koordinaten (x- und y-Wert) kann die Lage eines Punktes im zweidimensionalen Raum eindeutig bestimmt werden. In der Regel spielt auch die Höhe des Punktes, z.B. die Höhe über dem Meeresspiegel oder die Höhe über der Erdoberfläche, eine Rolle. Daher muss auch die dritte Raumdimension (z-Wert) berücksichtigt werden (vgl. Abb. 02-2).
Wird ein Geoobjekt durch einen Punkt repräsentiert, so genügt ein Punkt (x, y, z) im dreidimensionalen Raum für eine eindeutige Verortung. Häufig sind die in Karten oder GI-Systemen dargestellten Geoobjekte jedoch selbst mehrdimensional. Unter der Dimension eines Geoobjektes versteht man dabei die voneinander unabhängigen Raumrichtungen, die zur Darstellung des Geoobjektes verwendet werden (vgl. Abb. 02-3). Diese entsprechen den geometrischen Eigenschaften von Punkten, Strecken, Flächen und Körpern in einem kartesischen Koordinatensystem: * 0D Geoobjekte: Punkte (Orte); keine Längen und Flächen (z.B. Messstation, Bohrpunkt) * 1D Geoobjekte: Strecken; definiert durch eine Länge aber keine Fläche (Gewässerlängsprofil, vertikales Bodenprofil) * 2D Geoobjekte: Flächen; definieren eine geschlossene Linie (Sportplatz, Stadtgebiet, Einzugsgebiet) * 3D Geoobjekte: Körper; werden z.B. als Volumenkörper (Festkörper) oder als Grenzflächenkörper (Polyeder) definiert (Grundwasserkörper, Atmosphäre).

Neben den räumlichen Merkmalen sind Geoobjekte durch weitere Eigenschaften charakterisiert (z.B. kann einem Fluss ein Name zugeordnet sein, einer Stadt die Einwohnerzahl usw.). Diese Eigenschaften eines Geoobjekts, die nicht die räumliche Geometrie betreffen, werden als Attribute bezeichnet und bilden die thematische Dimension. Die zeitliche Veränderung von Geoobjekten oder Systemen wird in der Regel als vierte Dimension bezeichnet.
Die Lage im Raum (Topologie)
Für eine vollständige und korrekte Darstellung von Geoobjekten benötigen wir neben der Lage (Geometrie) und der thematischen Dimension auch die relative Lage der Objekte zueinander. Die relative Lage der Geoobjekte zueinander wird als Topologie bezeichnet. Sie zu bestimmen scheint zunächst einfach. Man kann sie aus der geometrischen Lage berechnen. Schwieriger wird es, wenn diese Punkte exakt die gleichen Raumkoordinaten haben und sich nur in der Höhenangabe (Dimensionalität) unterscheiden, wie z.B. in einem Gebäudeplan die Ausgänge eines Aufzuges, oder wenn es nicht auf die exakte Lage zueinander ankommt, sondern auf die Information, was benachbart ist. Ein bekanntes Praxisbeispiel für eine topologische Sichtweise ist ein Liniennetzplan, der in Abbildung 02-4 die Buslinien und Haltestellen für Marburg darstellt.
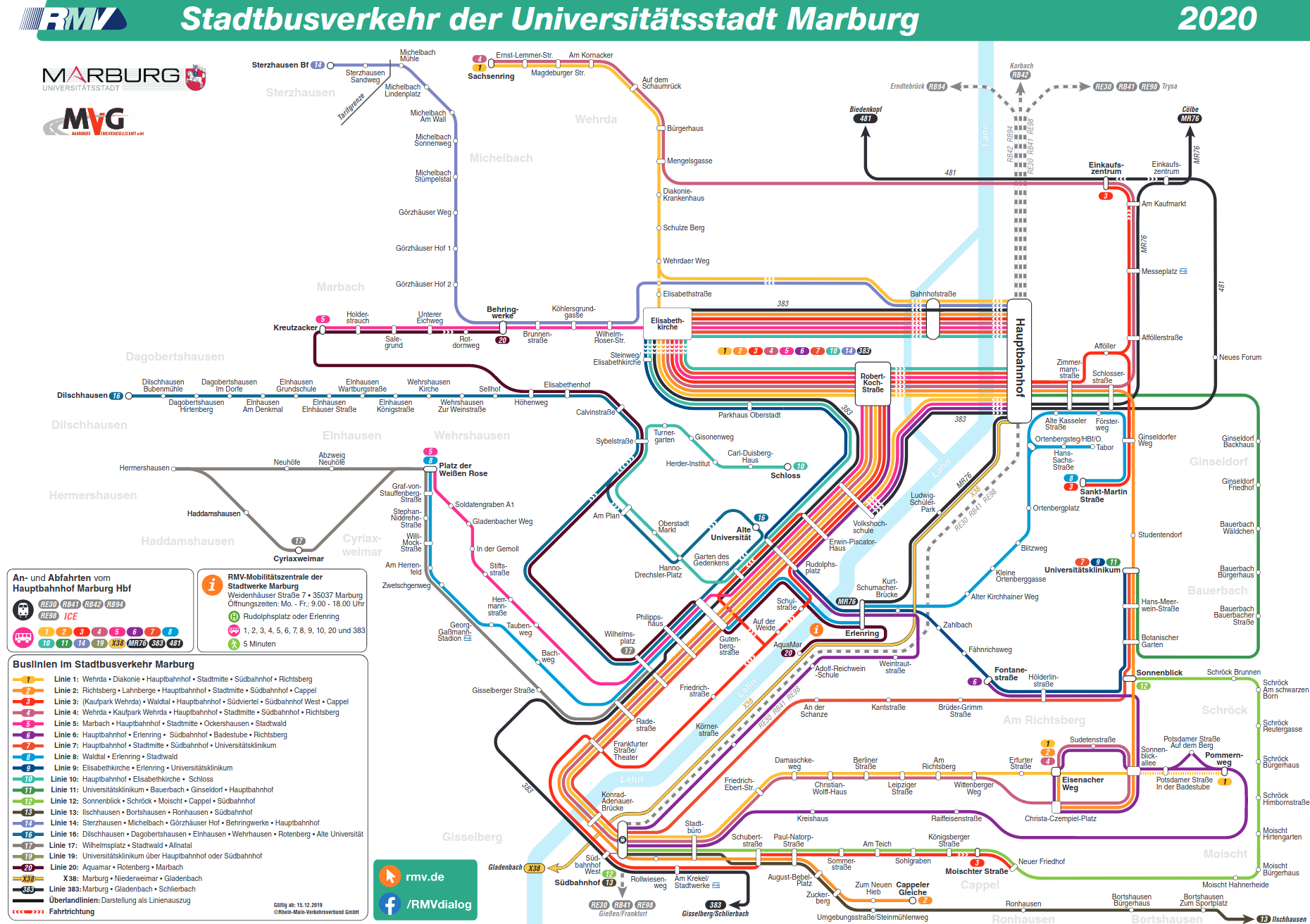
Geometrie, Dimensionen und Topologie
In vielen, wenn nicht in den meisten Situationen ist die korrekte Verknüpfung von Geometrie, Topologie und Dimension unerlässlich. Werden verschiedene Geoobjekte zu komplexen Einheiten verknüpft, kann es zu Überlappungen, Lücken oder anderen räumlichen Zuständen in der Abbildung der Realität kommen. Bei Karten kennen wir dieses Problem nicht, da die bildliche Darstellung der dargestellten Welt zwangsläufig zweidimensional ist und kartographische Symbole zur Verfügung stehen, um diesen Mangel darzustellen (z.B. Schraffen für die dritte Dimension Höhe). Im GIS hingegen stellen wir die Welt mehrdimensional dar. So können sich z.B. zwei Streckenabschnitte, die jeweils durch zwei Koordinaten definiert sind, kreuzen. Handelt es sich dabei um eine Bundesstraße und eine Autobahn, wird diese Kreuzung in der realen Welt durch eine Brücke realisiert. Im GI-System muss diese Brücke durch die exakte Geometrie, Topologie und Dimension im Sinne einer fehlenden Verbindung zwischen Autobahn und Bundesstraße dargestellt werden. Andernfalls kann es passieren, dass das Navigationsgerät die direkte Auffahrt auf die Autobahn verlangt, weil es die Brücke für eine Kreuzung hält, oder entgegen der Fahrtrichtung auf die Autobahn leitet.
Eine adäquate raum-zeitliche Beschreibung von Geoobjekten und ihren Eigenschaften erfordert daher, neben der Geometrie auch die Topologie und Dimension des Objektes bzw. des Raumkontinuums zu kennen und adäquat abzubilden.