Wir haben im Reader 01 festgestellt, dass sowohl diskrete Geoobjekte als auch mehrdimensionale Merkmalsausprägungen von Raumkontinua mit Hilfe von Koordinaten verortet und als Geodaten in Computern gespeichert werden können. Solche binären Geodaten stellen somit die geographische Repräsentation der Realität in GI-Systemen dar.
Die Grundlage für die Informationsreduktion bilden so genannte Datenmodelle. Ein Datenmodell entsteht durch die Abstraktion einzelner Objekte (Entitäten) und deren Eigenschaften (Attribute). Dabei werden gleichartige Objekte (z.B. Flüsse, Bundesstraßen, Stadtgebiete) zusammengefasst. Da die Grundlage aller GI-Systeme auf einer räumlichen Darstellung beruht, muss die bereits bekannte Geographische Abstraktion für ein besseres Verständnis der Datenmodellierung etwas umorganisiert und angepasst werden.

Die konkrete digitale bzw. technische Umsetzung ist mit diesem Konzept jedoch nicht geklärt. Die betrachteten Geoobjekte der realen Welt enthalten eine Informationsfülle, die gegen unendlich geht. Dies gilt erst recht für räumliche Kontinua, die je nach Maßstab beliebig komplex sein können. Für die digitale Repräsentation räumlicher Eigenschaften benötigen wir daher eine effiziente und einfache Methode zur Informations- bzw. Datenreduktion.

Die Abbildung zur Darstellung als Raster- und Vektordatenmodell verdeutlicht diesen zentralen Aspekt der Modellierung raumbezogener Daten. In der GIS-Anwendung haben sich hierfür zwei völlig unterschiedliche Datenmodelle etabliert, die als Rastermodell bzw. Vektordatenmodell bezeichnet werden. Beide Datenmodelle können prinzipiell sowohl zur Abbildung kontinuierlicher Eigenschaften als auch diskreter Geoobjekte verwendet werden. In der Praxis werden jedoch in der Regel kontinuierliche Daten im Rasterdatenmodell und diskrete Daten im Vektordatenmodell abgebildet. Beide Datenmodelle unterscheiden sich hauptsächlich in der Art der räumlichen Darstellung ihrer Merkmale, was auch in der Abbildung deutlich wird. Es ist zu beachten, dass die genannten Datenmodelle nicht nur für die Darstellung von zeitlich konstanten Merkmalsausprägungen, sondern auch für zeitlich veränderliche Merkmale verwendet werden können.
Das Vektordatenmodell
In einem kartesischen Koordinatensystem, das zur Darstellung der euklidischen Geometrie notwendig ist, können aus dem Grundelement Punkt beliebig komplexe räumliche Strukturen zur Modellierung von Geoobjekten aufgebaut werden. In der Schule haben Sie solche Punkte auch als Vektoren kennen gelernt, in der (Geo-)Informatik und im topologischen Kontext der Geographie spricht man von Knoten. Wenn wir zwei Knoten im Koordinatensystem referenziert haben, können wir diese Knoten durch eine Linie verbinden, die topologisch Kanten genannt wird. Wenn nicht nur zwei Knoten durch eine Kante verbunden sind, sondern durch die Verbindung von mindestens drei Knoten durch Kanten eine geschlossene Fläche entsteht, spricht man von einem Polygon bzw. topologisch von einem Netz. In GI-Systemen werden Knoten in der Regel als Punkte, nicht geschlossene Kantenverbindungen als Linien und Maschen als Polygone bezeichnet.

Das Rasterdatenmodell
Im Gegensatz zum Vektordatenmodell wird beim Rasterdatenmodell der Raum grundsätzlich durch zwei- oder dreidimensionale Objekte beliebiger Form und Größe, jedoch ohne gegenseitige Überlappung oder Lücken, repräsentiert. Die Merkmalsausprägungen werden als numerische Werte gespeichert, die jeder Zelle zugeordnet sind.
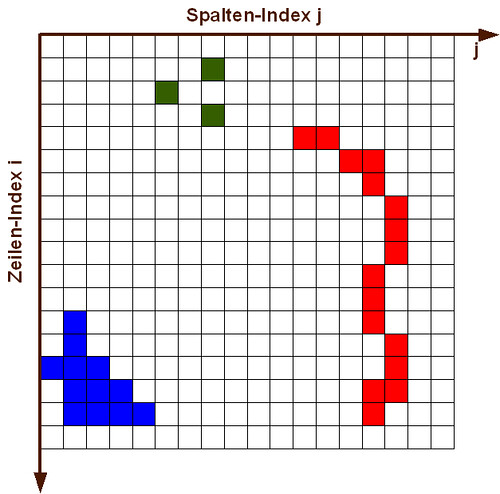
Obwohl möglich, kommen Rasterdatenmodelle mit unregelmäßig geformten Zellen in der GIS-Praxis kaum vor. Meist sind die Zellen in einer regelmäßigen Matrix, z.B. einem Gitter (Grid) aus Zeilen (horizontal) und Spalten (vertikal) angeordnet (vgl. Abbildung Rastermodell). In der Praxis werden regelmäßige Gitter fast ausschließlich als Quadrate (gelegentlich auch als Dreiecke oder Sechsecke) verwendet. Diese Quadrate werden im Zusammenhang mit Rasterdaten als Rasterzelle oder Pixel (“picture element”) bezeichnet.

Durch die überlappungsfreie Anordnung der Zellen in Zeilen und Spalten ergibt sich ein impliziter Raumbezug jeder Zelle. Dabei ist zu beachten, dass der Ursprung eines Rasterbildes immer in der linken oberen Ecke liegt und von dort in der Regel mit den beiden Laufindizes i, j durchgezählt wird. Damit ist jedes Pixel eindeutig identifizierbar. Auf diese Weise besteht für jedes Pixel auch ein expliziter Raumbezug. Für die Verortung in einem definierten kartesischen Koordinatensystem bzw. in der realen Welt ist der theoretische explizite Raum jedoch wenig hilfreich. Diese Verortung ist sowohl für die gemeinsame Nutzung von Rasterdaten mit Vektordaten als auch für die geographische Referenzierung der Rasterzellen zur realen Welt notwendig. Daher werden Rasterdatenmodelle grundsätzlich auch mit einem kartesischen Koordinatensystem versehen. Dieses hat jedoch seinen Ursprung (wie üblich) in der linken unteren Ecke. Die Rasterzellen können also sowohl über ihren Laufindex als auch über das kartesische Koordinatensystem im Raum identifiziert werden.