Ein bereits komplexes Beispiel für die Ableitung räumlicher Informationen ist die Sichtbarkeitsanalyse. Bei einer Sichtbarkeitsanalyse wird ausgehend von einem digitalen Höhenmodell und einem gegebenen Punkt berechnet, welche anderen Punkte im Gelände sichtbar sind. Das Prinzip der Sichtbarkeitsberechnung wird zunächst für den eindimensionalen Fall gezeigt und anschließend auf den zweidimensionalen Fall übertragen.
Anwendung Sichtbarkeitsanalyse
Sichtbarkeitsberechnungen werden in verschiedenen Anwendungen eingesetzt. Ein erstes Beispiel ist die Platzierung eines Aussichtsturms. Mit einem digitalen Geländemodell können in kurzer Zeit verschiedene Standorte geprüft werden. Außerdem kann die Berechnung mit verschiedenen Turmhöhen (Variation von hv) durchgeführt werden. Ein weiteres Beispiel ist die Ausbreitung elektromagnetischer Wellen (z.B. für die Planung von Mobilfunkantennen). Hier ist zu beachten, dass der Bereich, in dem elektromagnetische Signale empfangen werden können, nicht genau mit dem sichtbaren Bereich übereinstimmt. Im GIS wird dies in der Regel dadurch korrigiert, dass die Höhe eines Punktes um einen bestimmten Betrag unterhalb der Sichtlinie liegen muss, damit das Signal an diesem Punkt nicht empfangen werden kann. Dieser Betrag hängt von der Wellenlänge ab. Ein letztes Beispiel stammt aus der Wildbiologie. Hier kann ein GIS eingesetzt werden, um ein optimales Gebiet für die Wiederansiedlung von Tierarten auszuwählen. Das Rocky Mountain Bighorn Schaf zum Beispiel bevorzugt (unter anderem) Gebiete, die nur von wenigen Stellen aus eingesehen werden können. Dies verringert die Wahrscheinlichkeit, von einem Raubtier entdeckt zu werden.
Sichtbarkeitsanalyse Vektordatenmodell
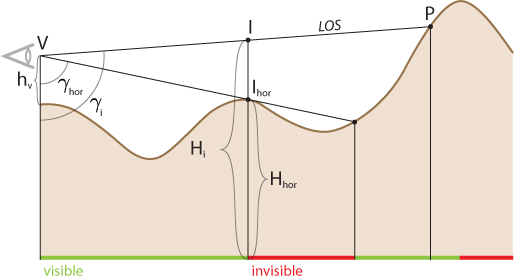
Im eindimensionalen Fall eines Profils wird zur Bestimmung der Sichtbarkeit eines Zielpunktes berechnet, ob ein Punkt zwischen dem Standort V und dem Zielpunkt P höher liegt als die Verbindungslinie (d.h. die Sichtlinie; engl. line of sight = LOS). Ist dies der Fall, so ist die Sichtlinie LOS blockiert und der Zielpunkt nicht sichtbar, andernfalls ist der Zielpunkt sichtbar. Am einfachsten lässt sich ein solcher Test programmieren, indem geprüft wird, ob die Steigung der Linie zwischen dem Standpunkt V und dem geprüften Zielpunkt P auf dem Profil größer oder kleiner ist als die der Linie zum zuletzt gespeicherten Horizontpunkt Ihor. Mit anderen Worten, ob der Vertikalwinkel γi zum aktuell geprüften Punkt größer (= sichtbar) oder kleiner (= unsichtbar) ist als der Vertikalwinkel γhor des letzten Horizonts.
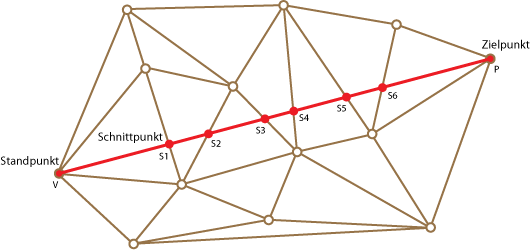
In einem linear interpolierten, dreiecksbasierten Geländemodell müssen zunächst die Höhen der Schnittpunkte der Verbindungslinien (von Start- und Zielpunkt) und der Dreiecksvermaschung berechnet werden, wie in der folgenden Abbildung dargestellt.
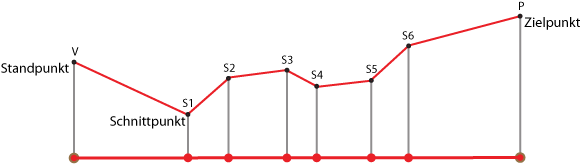
Die Höhen an den Schnittpunkten S1 bis Sn können durch lineare Interpolation aus den Höhen der beiden Dreieckspunkte berechnet werden, die die betreffende Dreieckskante abschließen. Das Ergebnis ist ein Profil wie im eindimensionalen Fall (siehe Abbildung unten). Auf dieses Profil kann nun der gleiche Algorithmus zur Bestimmung der LOS wie oben angewendet werden.
Rasterbasierte Sichtbarkeitsanalyse
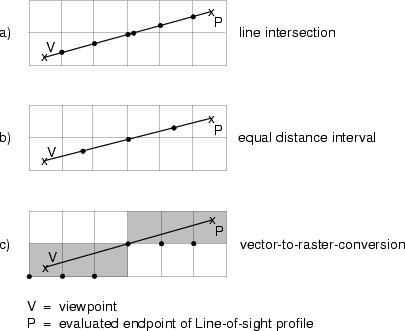
Die Bestimmung von Profilen zwischen dem Standpunkt V und dem Zielpunkt P in einem rasterbasierten Geländemodell (Raster) ist ein Sonderfall der Dreiecksvermaschung: Hier kann analog die Verbindungslinie der durch das Raster gebildeten Quadrate (anstelle der Dreiecke) geschnitten und ein Profil erstellt werden (Abbildung a). Da die Berechnung der Schnittpunkte je nach Rasterauflösung sehr rechenintensiv sein kann, gibt es Näherungsalgorithmen zur Berechnung eines Profils. Zwei davon sind in der folgenden Abbildung dargestellt: In Abbildung b) wird die Höhe entlang der Sichtlinie in regelmäßigen Abständen abgefragt und gespeichert. Da jede Gitterzelle genau eine Höhe hat, muss nur berechnet werden, in welcher Gitterzelle der betreffende Zwischenpunkt liegt. Bei der Lösung in Abbildung c) wird zuerst der Sichtstrahl gerastert und dann die Höhe der so entstandenen Rasterzellen mit denen des Geländemodells verglichen.