Geographische Koordinaten
Die vorstehenden Beispiele zeigen, wie mühsam und fehleranfällig die Orientierung an Objekten und ihren Namen ist. Sie zeigen auch, dass messbare, d.h. geometrisch maßstäbliche Bezugssysteme nicht unbedingt geographisch lokalisierbar sein müssen. Im Kapitel über Raumrepräsentationen wurde der Bogen von der abstrakten Definition des Raumes und seiner Objekte bis hin zur Repräsentation geographischer Informationen in spezifischen Datenobjekten gespannt. Nun geht es darum, diese beiden Konzepte zusammenzuführen.
Ein leistungsfähiges System zur Referenzierung von geographischen Räumen sollte unbedingt die folgenden grundlegenden Eigenschaften vereinen:
- Skalenunabhängige Identifikation jedes Punktes auf der Erdoberfläche
- Messbarkeit, d.h. mathematische Berechnungsvorschriften für alle geometrischen Operationen
- Zuweisung aller beliebig skalierten Attribute (z.B. Name, Temperatur, Qualität)
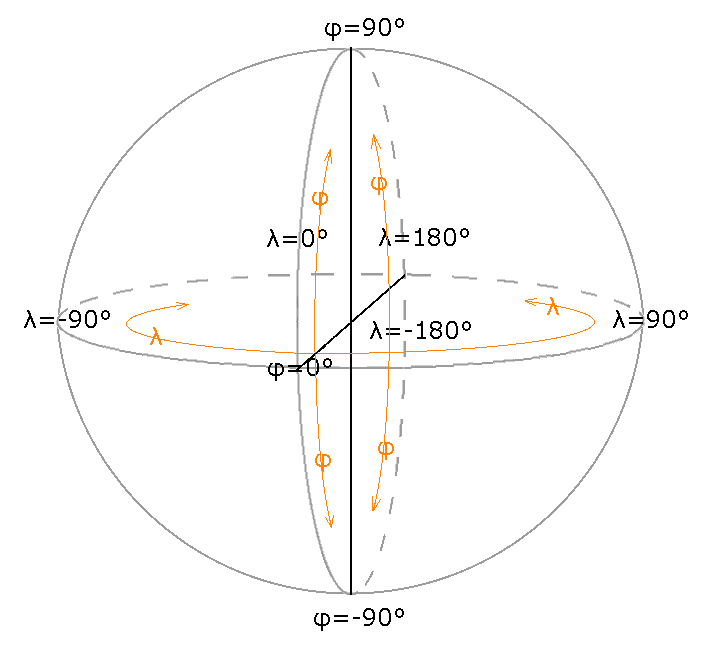
Die Erde ist in erster Näherung eine Kugel. Daher ist es naheliegend, Punkte auf der Oberfläche durch Kugelkoordinaten zu definieren. Da die Oberfläche einer Kugel bekannt ist, genügen zur Bestimmung eines Punktes die beiden Winkel für den Azimut (geographische Länge) Lambda und den Zenit (geographische Breite) Phi (Abb. 03-07).

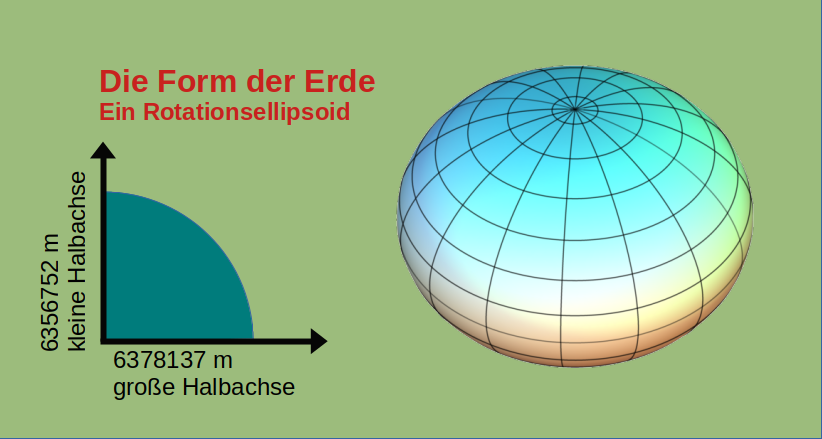
Überträgt man das Konzept der Kugelkoordinaten auf die Erde, so ergeben sich eine Reihe von Problemen. Das augenfälligste ist die Abplattung der Erde an den Polen, die durch die Erdrotation verursacht wird. Für die Längenbestimmung ist die Tatsache, dass die Erde ein Rotationsellipsoid mit großen und kleinen Halbachsen ist, unerheblich. Anders verhält es sich bei der Bestimmung der geographischen Breite, da sich die Halbachsen der Erde um ca. 21,4 km unterscheiden (Abb. 03-08).
Die Abbildung zeigt das Rotationsellipsoid der Erde mit kreisförmigen Breitenkreisen (in der Äquatorebene Radius der großen Halbachse) und Längenkreisen (kleine Halbachse an den Polen). Das daraus resultierende Maß für die Exzentrizität von ca. 1:298 gibt die Abplattung der Erde und damit die Streckenverschiebung bei der Bestimmung der sphärischen Koordinaten an. Das zentrale Problem der exakten Bestimmung der Erdoberfläche (im Sinne einer homogenen Oberfläche für die Berechnung der sphärischen Koordinaten) liegt nun in der Entscheidung, welche mathematische Darstellung eines Ellipsoids als geeignetes Modell für das reale Rotationsellipsoid der Erde verwendet wird.
Da es sich immer nur um eine Annäherung an die ideale Erdform bezogen auf ein bestimmtes Erdgebiet handelt, ist die Eignung des gewählten Ellipsoids als Referenz (Bezugsellipsoid) für die Berechnung der Vermessungsnetze (Koordinatensysteme) und der daraus abgeleiteten Projektionssysteme von entscheidender Bedeutung (Abb. 03-09).
Ellipsoide und Bezugssysteme
In den letzten zwei Jahrhunderten wurden sehr unterschiedliche Referenzellipsoide entwickelt. Vor allem um regionale oder nationale Kartenwerke genauer erstellen zu können. Heute ist die Annäherung der Erdfigur an die geometrische Figur eines Ellipsoids relativ einfach durchzuführen. Um eine möglichst genaue Lage zu erhalten, werden alle gemessenen Punkte senkrecht auf das gewählte Bezugsellipsoid projiziert. Für kleinräumige Betrachtungen ist die erreichbare Genauigkeit völlig ausreichend. Besuchen Sie die offizielle [Online Datenbank für Bezugssysteme] (http://www.epsg.org). Navigieren Sie zum EPSG Geodetic Parameter Set und suchen Sie nacheinander nach den Begriffen Bessel, Clarke, Krassowski und WGS84. Klicken Sie auf den View Link und vergleichen Sie die verfügbaren Parameter.
Das geodätische Datum
Für kleinräumige Betrachtungen ist die Genauigkeit einer auf ein Referenzellipsoid bezogenen Koordinatenbestimmung völlig ausreichend. Interessanterweise wurde erst mit der Entwicklung der Interkontinentalraketen in der ersten Hälfte des 20. Jahrhunderts eine neue Genauigkeitsdimension für die praktische Anwendung angestrebt. In der Anwendung ist eine senkrechte Projektion auf das Ellipsoid nicht möglich. Die Senkrechtprojektion auf das auf Meereshöhe angenäherte Ellipsoid weicht um die sogenannte Lotabweichung von der wahren Senkrechten ab, wie sie durch das Gravitationslot dargestellt wird. Bei Messungen, die genauer als etwa 0,5 m/1000 m sein sollen (z.B. zur Berechnung der Ballistik von Interkontinentalraketen oder der Kontinentaldrift…), muss dieser Effekt berücksichtigt und die Messung korrigiert werden (Abb. 03-10).

Das Bezugsmodell für die räumlich (und auch zeitlich) variierende Erdschwere ist das sogenannte Geoid. Die Abbildung des Erdschwerefeldes visualisiert diese Schwereanomalien stark überhöht und farblich hervorgehoben.

Für genaue Messungen oder möglichst genaue Kartenprojektionen müssen beide Bezugskörper, das Ellipsoid und das Geoid, berücksichtigt werden. Die Abbildung der Schwerevariation und eine weitere Alternative zeigen die konzeptionellen Probleme bei der Berücksichtigung von Geoid und Referenzellipsoid für eine exakte Koordinatenberechnung. In der klassischen Vermessungstechnik wird dazu ein Referenzpunkt (Fundamentalpunkt) möglichst im Zentrum des abzubildenden Erdausschnitts festgelegt, der zusammen mit dem Referenzellipsoid das sogenannte geodätische Datum ergibt.
Das geodätische System
Seit der satellitengestützten Vermessung mit Global Positioning Systems (GPS) liegen viele, von der realen Erdfigur unabhängige Messungen vor, so dass man nicht mehr vom geodätischen Datum, sondern vom geodätischen System spricht.
Das World Geodetic System 1984 (WGS 84) ist heute das am weitesten verbreitete geodätische Bezugssystem und dient als einheitliche Grundlage für Positionsangaben auf der Erde und im erdnahen Weltraum. Geodätische Systeme sind im Gegensatz zum geodätischen Datum global konstruiert und bestehen aus dem Referenzellipsoid, dem eingemessenen Geoid, und zwölf Fundamentalstationen, über die der Bezug zur Erdkruste durch zeitabhängige Koordinaten bestimmt wird.
Betrachten Sie die Abbildung zu den Referenzellipsoiden. Sie zeigt schematisch (zweidimensional) die Verschiebungen der Referenzellipsoide gegenüber dem Geoid, also der wahren Erdoberfläche. Die Sterne markieren das Zentrum des jeweiligen Körpers. Versuchen Sie herauszufinden, welche Parameter notwendig sind, um diese Verschiebung zu erreichen.
Kartenprojektionen in GI-Systemen
Die geographischen Längen- und Breitengrade referenzieren jeden Punkt auf der Erdoberfläche mit hoher, skalierbarer Genauigkeit. Sie beziehen sich auf die wohldefinierte, dreidimensionale, idealisierte Oberfläche der Erde. Diese Figur der Erde verwendet bekannte und durch Konvention festgelegte Referenzpunkte: das Royal Observatory in Greenwich für den Referenzmeridian, den Erdmittelpunkt und die Halbachsen des Referenzellipsoids der Erde als Annäherung an ihre wahre Form.
Mit Hilfe dieser Parameter ist eine hinreichend genaue Lokalisierung aller Geoobjekte möglich. Gleiches gilt für die Analyse und Berechnung ihrer geometrischen Beziehungen. Historisch wurden diese Aufgaben nicht auf einem Sphäroid, sondern auf zweidimensionalen Karten als projiziertes Abbild der Erde durchgeführt. Auch heute noch besteht für sehr viele Anwendungen und Daten die Notwendigkeit, eine nivellierte zweidimensionale Projektion der Erdoberfläche zu verwenden. Daher sind
- alle Ein- und Ausgangskarten zweidimensional
- alle Rasterdatensätze (Satellitendaten, Luftbilder) zweidimensional, da sich quadratische Raster nicht verzerrungsfrei und ohne Überlappungen oder Lücken auf eine Kugel auftragen lassen.
Die Kartenprojektion ist nun ein mathematisches Verfahren, mit dem die gekrümmte Oberfläche der dreidimensionalen Erde auf die ebene, zweidimensionale Karte übertragen wird. Dies geschieht in zwei Schritten:
- Auswahl eines geeigneten Referenzmodells für die Kugelform der Erde
- Transformation der geographischen Koordinaten (Länge und Breite) in ein kartesisches Koordinatensystem (x und y bzw. Rechtswert und Hochwert).
Im euklidischen Raum wird durch die Bestimmung der x,y-Koordinate ein Punkt in der Ebene (=zweidimensional) lokalisiert. Obwohl der dreidimensionale euklidische Raum auch die durch geographische Winkel bestimmten Positionen abbilden kann, ist aus den oben genannten Gründen die Projektion von sphärischen Koordinaten in ein zweidimensionales kartesisches Bezugssystem üblich und meist auch sinnvoll.
Kartenprojektionen können somit als Transformation von sphärischen Koordinaten der geographischen Länge und Breite in kartesische Koordinaten y,x (Hochwert, Rechtswert) verstanden werden.
Da es sich bei allen Transformationen um sphärische Trigonometrie handelt und Geodatensätze auf beliebig unterschiedlichen Referenzellipsoiden und/oder geodätischen Systemen basieren (können), ist es für die Arbeit mit GI-Systemen unerlässlich, diese Parameter und ihre Eigenschaften zu kennen und interpretieren zu können.
Kartenprojektionen werden üblicherweise nach der Projektionsfläche, der Lage der Projektionsfläche oder den Abbildungseigenschaften klassifiziert. Da es in GI-Systemen vor allem auf Genauigkeit und Qualität ankommt, ist die Klassifizierung nach den Abbildungseigenschaften von besonderer Bedeutung. Projektionen müssen die abgebildeten Flächen der Erdoberfläche verzerren. Es gibt keine 1:1 Projektion von Orten und Flächen aus einem dreidimensionalen Bezugssystem auf eine zweidimensionale Karte:
- Längentreue Projektion (engl.: equidistance): Maßstabsgetreue Entfernungen auf der Karte
- flächentreue Projektion (engl.: equal area): maßstabsgetreue Flächeninhalte auf der Karte
- Winkeltreue Projektion (engl.: conformity): Genaue Darstellung von Winkeln auf der Karte
- vermittelnde Projektion: Kompromiss zwischen Längentreue, Flächentreue oder Winkeltreue
Die daraus resultierenden Qualitätseinbußen müssen je nach Zielsetzung und Fragestellung die Kriterien für die Auswahl eines geeigneten Projektionsverfahrens bestimmen. Da alle drei Kriterien nicht erfüllbar sind (außer auf einem maßstäblich verkleinerten exakten dreidimensionalen Abbild der Erde), wurden verschiedene Projektionsverfahren und Referenzkörper entwickelt, um diese Fehler zu minimieren.