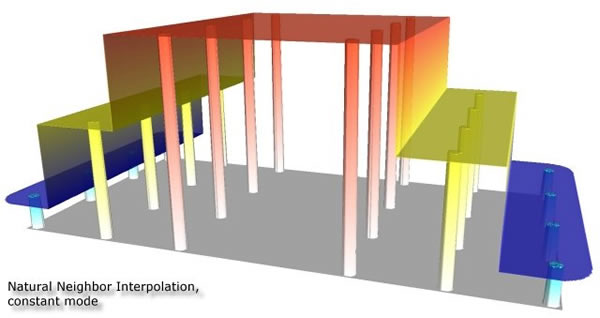
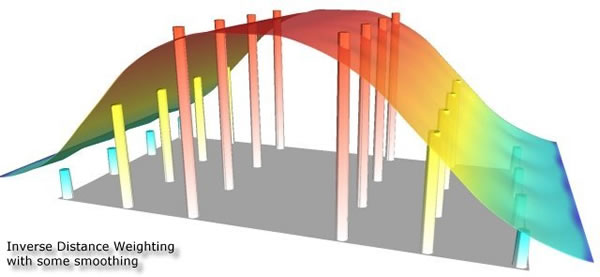
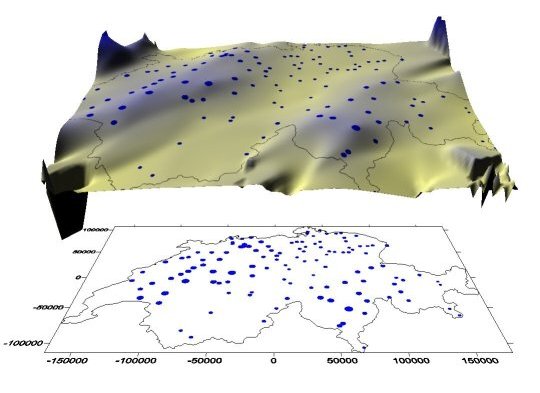
Betrachten Sie zunächst eine andere Darstellung der Ihnen bereits bekannten Abbildung der Niederschlagsmessstationen in der Schweiz. Im oberen Teil sehen Sie eine 3D-Niederschlagsfläche. Die blauen Punkte sind wiederum die Standorte der Messstationen, ihre Grösse entspricht der Niederschlagsmenge. Die unterschiedlichen Höhen der Fläche und ihre Färbung hängen ebenfalls mit der Niederschlagsmenge zusammen. Im unteren Teil sehen Sie die 2D Lage der Messstationen in der Schweiz.
Bei der Erstellung einer kontinuierlichen Fläche aus einzelnen Punktbeobachtungen, wie z.B. Niederschlagsmessungen an 100 verschiedenen Punkten, stehen zentrale Fragen im Vordergrund: Wie können diese Punktdaten in eine kontinuierliche Flächendarstellung überführt werden, welche Methoden und Werkzeuge sind dafür notwendig und welches Wissen wird vorausgesetzt?
Der erste Schritt bei der Analyse solcher kontinuierlichen Variablen beginnt typischerweise mit der Erstellung einer räumlichen Stichprobe. Dabei werden Messpunkte festgelegt, die für das zu untersuchende Phänomen repräsentativ sind. Von besonderer Bedeutung sind dabei die Repräsentativität, die Homogenität hinsichtlich der räumlichen Abhängigkeiten und die räumliche Verteilung der Messpunkte. Die Repräsentativität stellt sicher, dass alle relevanten Ausprägungen des Phänomens, einschließlich der Minima und Maxima, in der Stichprobe vertreten sind. Die Homogenität (oder Stationarität) stellt sicher, dass die Messwerte miteinander vergleichbar sind, während die räumliche Verteilung der Messungen (zufällig, regelmäßig oder in Gruppen) und die Größe der Stichprobe die Aussagekraft der Ergebnisse beeinflussen.
Um aus Punktbeobachtungen eine kontinuierliche Fläche zu erstellen, wie im Beispiel des Niederschlags, müssen grundlegende Überlegungen bei der Planung und Analyse der Daten berücksichtigt werden:
Repräsentativität: Es ist wichtig, dass die Stichprobe alle relevanten Ausprägungen des Phänomens repräsentiert. Dazu gehören insbesondere die Extremwerte (Minima und Maxima). Damit wird sichergestellt, dass das gesamte Spektrum des untersuchten Phänomens in die Analyse einfließt.
Homogenität: Die räumliche Abhängigkeit zwischen den Datenpunkten muss im gesamten Untersuchungsgebiet konsistent sein. Dies bedeutet, dass die Messwerte zweier Stationen, die beispielsweise 2 km voneinander entfernt sind, überall im Untersuchungsgebiet ähnlich sein sollten, egal ob im Tessin, im Jura, in Graubünden oder in Freiburg. Diese Übereinstimmung wird als „Stationarität“ bezeichnet.
Räumliche Verteilung der Messungen: Die Anordnung der Messpunkte kann zufällig, regelmässig oder geclustert sein. Diese Verteilung ist für die Interpretation und die statistische Analyse der Daten von grosser Bedeutung. Mit Hilfe von Techniken wie der „Nearest Neighbor“-Statistik, die Teil der „Point Pattern Analysis“ ist, kann die räumliche Verteilung der Messpunkte charakterisiert und analysiert werden.
Größe (= Anzahl der Messungen): Die Anzahl der Messpunkte hängt vom Phänomen und von der Größe des Untersuchungsgebietes ab. Praktische Einschränkungen wie die Zugänglichkeit des Geländes oder die Kosten der Messungen können die Anzahl der Messpunkte ebenfalls beeinflussen. Es ist oft schwierig, die ideale Stichprobengröße zu bestimmen, da sie von vielen Faktoren abhängt.
Diese Überlegungen sind entscheidend, um aus punktuellen Daten eine valide und aussagekräftige kontinuierliche Flächendarstellung zu generieren. Sie helfen nicht nur bei der Erstellung der Fläche, sondern stellen auch sicher, dass die resultierende Fläche das untersuchte Phänomen adäquat und genau repräsentiert. Diese Ansätze sind entscheidend für den Übergang von punktuellen Beobachtungen zu einer flächenhaften, räumlich kontinuierlichen Darstellung unter Berücksichtigung stochastischer Schwankungen und mathematischer Näherungen.
Zur statistischen Analyse der räumlichen Verteilung der Messungen können Methoden wie die „Nearest Neighbor“-Statistik verwendet werden. Diese gehört zu den „Point Pattern Analysis“-Techniken, mit deren Hilfe die räumliche Verteilung der Messpunkte charakterisiert und analysiert werden kann.
Repräsentativität, Homogenität, räumliche Verteilung und Grösse hängen zusammen. So ist eine Grösse (Anzahl) von 5 Messstationen für die Schätzung des gesamtschweizerischen Niederschlags kaum sinnvoll und damit nicht repräsentativ. Ebenso wenig repräsentativ wäre die Auswahl aller deutschschweizerischen Messstationen für die gesamtschweizerische Schätzung. Hier würde vielleicht die Grösse ausreichen, nicht aber die räumliche Verteilung. Würde man nun alle Stationen unter 750 mNN auswählen, so wäre zwar die Stichprobe sowohl von der Größe als auch von der räumlichen Verteilung her in Ordnung, aber das Phänomen wäre in der Stichprobe nicht homogen repräsentiert. Eine anschließende Schätzung würde vor allem im Bereich über 750 mNN deutlich verzerrt ausfallen.
Räumliche Interpolation von Daten
Nachdem wir uns kurz mit dem Zusammenhang von räumlichen Abhängigkeiten beschäftigt haben, kommen wir nun zu räumlichen Interpolationen. Was sind räumliche Interpolationen? Darunter versteht man die Berechnung unbekannter Werte auf der Basis benachbarter bekannter Werte. Die meisten dieser Techniken gehören zu den komplexeren Methoden der räumlichen Analyse, daher beschränken wir uns hier bewusst auf einen prinzipiellen Überblick über die Methoden.
Inverse Distanzgewichtung, Spline-Interpolation, Kriging-Methoden, Polynomiale Regressionsmethoden sind nur einige der sehr gebräuchlichen Interpolationsmethoden, die in GIS-Software zu finden sind.
Lokale vs. Globale Interpolation
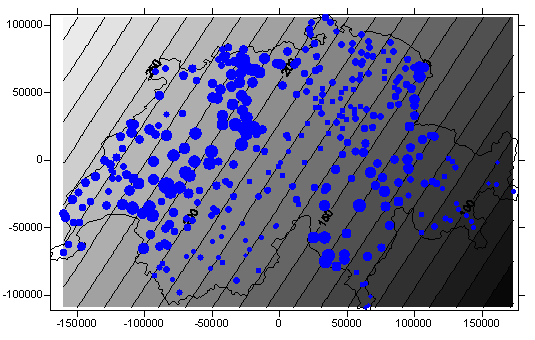
Globale Methoden werden auf ALLE Daten im Untersuchungsgebiet angewendet, lokale Methoden nur auf räumlich definierte Teilmengen. Globale Interpolation ist daher nicht geeignet, um möglichst exakte Werte zu ermitteln, sondern um globale räumliche Strukturen zu beurteilen.
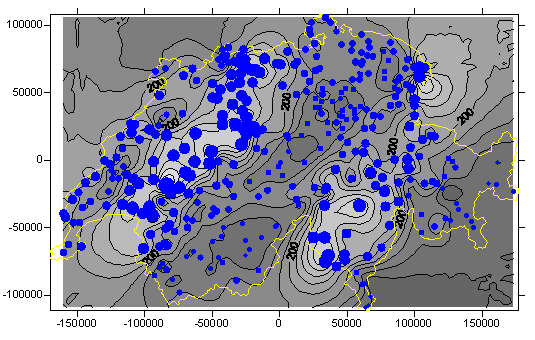
Als Beispiel ist unten eine lineare Trendfläche dargestellt - sie wurde mittels Regression aus den Niederschlagsdaten der Schweiz ermittelt und zeigt einen Trend zur Zunahme der Niederschlagshöhen von SE nach NW. In der Abbildung darunter wurde aus den gleichen Daten eine lokale Interpolation mittels sogenannter Radial-Base-Interpolation durchgeführt.
Exakte vs. nicht-exakte Interpolation
Exakte Interpolation bedeutet, dass die geschätzte Fläche durch die bekannten Punkte verläuft, während bei nicht exakten Methoden die Schätzwerte für bekannte Beobachtungen von den tatsächlichen Werten abweichen können. Letztere Methoden sind dann sinnvoll, wenn die bekannten Daten bereits eine gewisse Unsicherheit aufweisen.